ε-δ論法(イプシロンデルタろんぽう、(ε, δ)-definition of limit)は、解析学において、(有限な)実数値のみを用いて極限を定義する方法である。
https://ja.wikipedia.org/wiki/イプシロン-デルタ論法
以下では、筆者はイプシロン・デルタ論法に対する現時点での著者の認識を提示する。なお、彼は関数の極限と関数の連続性をうまく認識していない。なお、彼はイプシロン・デルタ論法を理解していないので、盛大に間違っている可能性が高い。だから、君らはきちんとした情報に当たろう。
1.0 イプシロン・デルタ論法
1.1 定義
1.1(俺系統の認識) 任意の実数εに対して、ある実数δが存在する、かつ変数xとある定点aとの差の絶対値がその実数δよりも小さいならば、関数値f(x)と関数値f(a)との差の絶対値が実数εよりも小さい。
|x-a|<δ→|f(x)-f(a)|<ε。個人的には、彼はx’とy’を使用して、上記を次のように書き換えたい。任意の実数y’に対して、ある実数x’が存在する、かつ変数xとある定点aとの差の絶対値がその実数x’よりも小さいならば、関数値f(x)と関数値f(a)との差の絶対値が実数y’よりも小さい。
または、彼は時刻tと位置xを使用して、上記を次のように書き換えたい。任意の距離xに対して、ある時間が存在する、かつ時刻tとある定点aとの差の絶対値がその時間tよりも小さいならば、関数値f(t)と関数値f(a)との差の絶対値が距離xよりも小さい。なお、位置差を距離と置き、時刻差を時間と置いた。
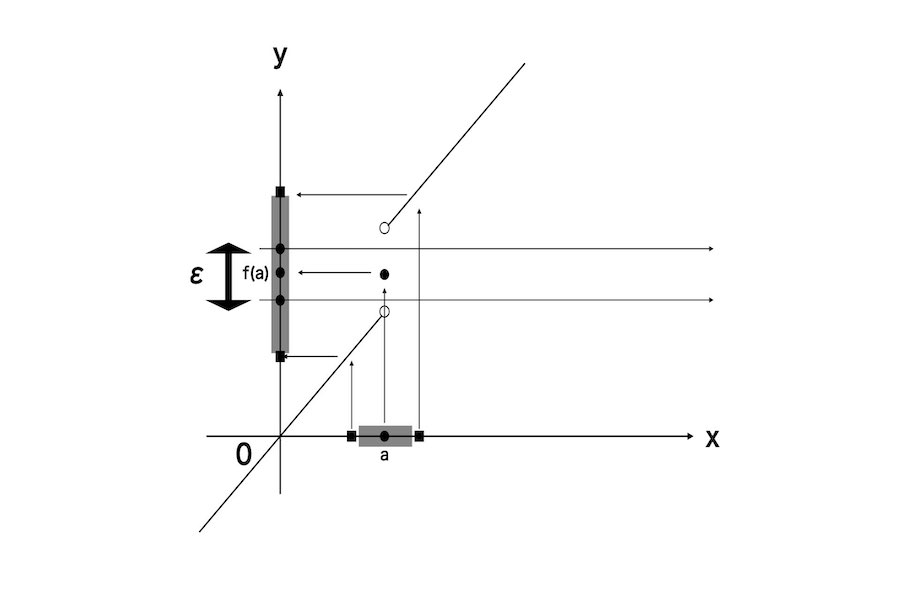
上記が定点aでの不連続な状態である。ある実数εに対して、ある実数δが存在しない、または変数xとある定点aとの差の絶対値がその実数δよりも小さい、関数値f(x)と関数値f(a)との差の絶対値が実数εよりも小さくない。
黒い両矢印がεである。δがx軸の上の半透明な黒帯である。y軸の上の半透明な黒帯は。たとえ彼がどんなに小さな黒い帯を取るとしても、その帯に対応するy軸の上の半透明な黒帯はεを超えてしまう。彼がどんなδの取り方をしても、その帯に対応するy軸の上の半透明な黒帯はεを超えてしまう。この状態が不連続である。
1.2 具体例と例題

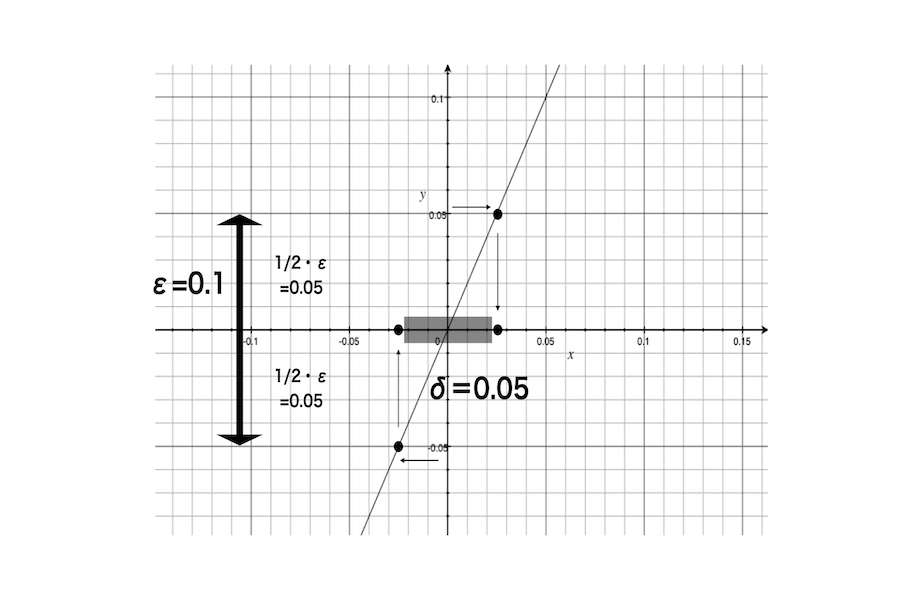
彼は関数y=xの原点における関数の連続性を考える。|x-0|<δ→|f(x)-f(0)|<ε。f(x)はxであり、f(0)は0であるので、|x-0|<δ→|x-0|<ε。今、彼はεを0.1とする。この時、上記の式は|x-0|<δ→|x-0|<0.1。この時、もし彼がδを0.1と取るならば、上記の式は|x-0|<0.1→|x-0|<0.1となり、式が満足される。つまり、不等式を満足するようなδが存在する。
上記の図も同様である。彼はεを0.1とする。図における黒い両矢印のように、彼がεを0.05から-0.05までと解釈すると、それに対応するδの範囲も0.05から-0.05までである。この時、半透明の黒帯の部分がδに対応する。視覚的には、δが存在している。
ただ、彼がδを0.1とすると、|x-0|<0.1→|x-0|<0.1の時、xを0.09と取ることができるように思える。すると、x=0.09は半透明の黒帯の部分からはみ出しているように思える。しかし、こん不等式それ自体は満足されていつ。だから、彼はδを2で割って、0.05(ε/2)とすると、x=0.09/2=0.045は半透明の黒帯の部分からはみ出さない。
まとめると、彼がδを(1/2)εと取るとき、そのδは上記の不等式を満足する。この時、関数y=xは原点で連続である。
彼は関数y=2xの原点における関数の連続性を考える。|x-0|<δ→|f(x)-f(0)|<ε。f(x)は2xであり、f(0)は0であるので、|x-0|<δ→|2x-0|<ε。今、彼はεを0.1とする。この時、上記の式は|x-0|<δ→|2x-0|<0.1。この時、もし彼がδを0.1/2=0.05と取るならば、上記の式は|x-0|<0.05→|x-0|<0.1となり、式が満足される。つまり、不等式を満足するようなδが存在する。
上記の図も同様である。彼はεを0.1とする。図における黒い両矢印のように、彼がεを0.05から-0.05までと解釈すると、それに対応するδの範囲も0.025から-0.025までである。この時、半透明の黒帯の部分がδに対応する。同様に視覚的には、δが存在している。
図1.21を見るとわかるように、y=xの時と比較すると、半透明の黒帯の長さはより短くなった。なぜなら、y=2xはy=xよりも大きく変動するので、たとえεが同じであるとしても、彼はより小さいδを取る必要がある。上記と同様に、彼はδを2で割って、0.025(ε/2)として、半透明の黒帯の部分からはみ出さないようにしたい。
まとめると、彼がδを(1/4)εと取るとき、そのδは上記の不等式を満足する。この時、関数y=2xは原点で連続である。
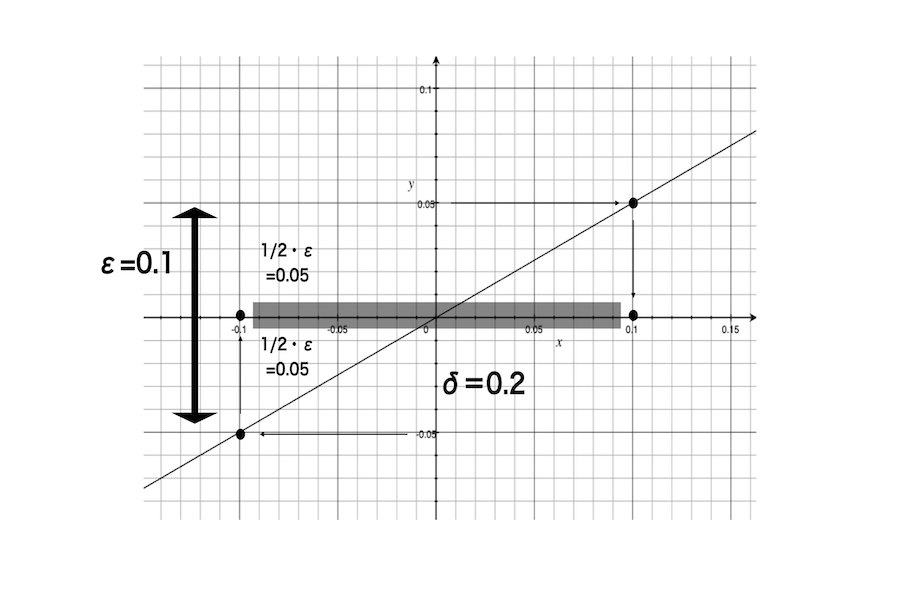
彼は関数y=(1/2)xの原点における関数の連続性を考える。|x-0|<δ→|f(x)-f(0)|<ε。f(x)は(1/2)xであり、f(0)は0であるので、|x-0|<δ→|(1/2)x-0|<ε。今、彼はεを0.1とする。この時、上記の式は|x-0|<δ→|(1/2)x-0|<0.1。この時、もし彼がδを0.2と取るならば、上記の式は|x-0|<0.2→|x-0|<0.1となり、式が満足される。つまり、不等式を満足するようなδが存在する。
上記の図も同様である。彼はεを0.1とする。図における黒い両矢印のように、彼がεを0.05から-0.05までと解釈すると、それに対応するδの範囲も0.1から-0.1までである。この時、半透明の黒帯の部分がδに対応する。同様に視覚的には、δが存在している。
図1.21を見るとわかるように、y=x及びy=2xの時と比較すると、半透明の黒帯の長さはより長くなった。なぜなら、y=(1/2)xはy=xよりもゆっくりと変動するので、たとえεが同じであるとしても、彼はより大きなδを取っても大丈夫である。上記と同様に、彼はδを2で割って、0.1(ε/2)として、半透明の黒帯の部分からはみ出さないようにしたい。
まとめると、彼がδをεと取るとき、そのδは上記の不等式を満足する。この時、関数y=(1/2)xは原点で連続である。
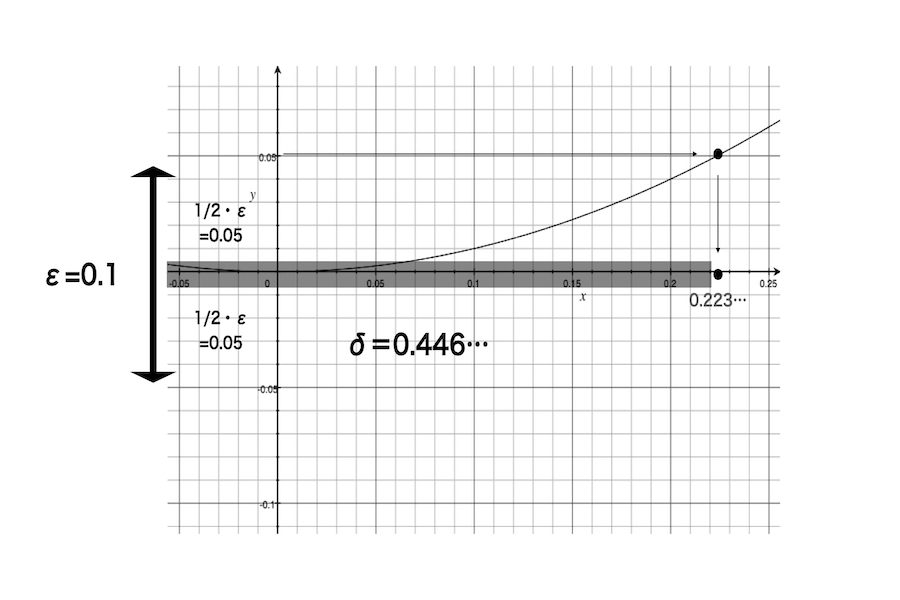
彼は関数y=x^2の原点における関数の連続性を考える。|x-0|<δ→|f(x)-f(0)|<ε。f(x)はx^2であり、f(0)は0であるので、|x-0|<δ→|x^2-0|<ε。今、彼はεを0.1とする。この時、上記の式は|x-0|<δ→|x^2-0|<0.1。この時、もし彼がδを0.446…=√0.1と取るならば、上記の式は|x-0|<0.446…→|x^2-0|<0.1となり、式が満足される。つまり、不等式を満足するようなδが存在する。
上記の図も同様である。彼はεを0.1とする。図における黒い両矢印のように、彼がεを0.05から-0.05までと解釈すると、それに対応するδの範囲も0.223…から-0.223…までである。この時、半透明の黒帯の部分がδに対応する。同様に視覚的には、δが存在している。
上記と同様に、彼はδを2で割って、0.223…として、半透明の黒帯の部分からはみ出さないようにしたい。図1.21を見るとわかるように、y=x及びy=2x及びy=(1/2)xの時と比較すると、半透明の黒帯の長さはより長くなった。
まとめると、彼がδを(√ε)/2と取るとき、そのδは上記の不等式を満足する。この時、関数y=x^2は原点で連続である。

彼は関数y=1の原点における関数の連続性を考える。|x-0|<δ→|f(x)-f(0)|<ε。f(x)は1であり、f(0)は1であるので、|x-0|<δ→|1-1|<ε。今、彼はεを1とする。この時、上記の式は|x-0|<δ→|0|<1。たとえ彼がどんなδを取るとしても、不等式は満足される。例えば、彼が4をδとして取るとしても、関数値の差は0になるので、その差はεの範囲に収まる。つまり、不等式を満足するようなδが存在する。
上記の図も同様である。彼はεを1とする。図における黒い両矢印のように、彼がεを1.5から0.5までと解釈すると、それに対応するδの範囲は全てである。この時、半透明の黒帯の部分がδに対応する。同様に視覚的には、δが存在している。視覚的に見ると、εに対応するδは存在しないように見えるが、どんなデルタを取るとしても、不等式は成り立つ。
1.3 改良形?
1.3(俺系統の認識) 任意の実数εに対して、ある実数δが存在する、かつ(定点aと(1/2)δの和)と(定点aと(1/2)δの差)の和が(定点aと(1/2)δの和)の逆写像と(定点aと(1/2)δの差)の逆写像よりも小さいならば、関数値f(a+(1/2)δ)と関数値f(a-(1/2)δ)の差は(関数値f(a)と(1/2)εの和)と(関数値f(a)と(1/2)εとの差)の和よりも小さい。
a+(1/2)δ-(a-(1/2)δ)<f^-1(f(a)+(1/2)ε)-f^-1(f(a)+(1/2)ε)→f(a+(1/2)δ)-f(a-(1/2)δ)<f(a)+(1/2)ε-(f(a)-(1/2)ε)。変形すると、δ<f^-1(f(a)+(1/2)ε)-f^-1(f(a)+(1/2)ε)→f(a+(1/2)δ)-f(a-(1/2)δ)<ε。
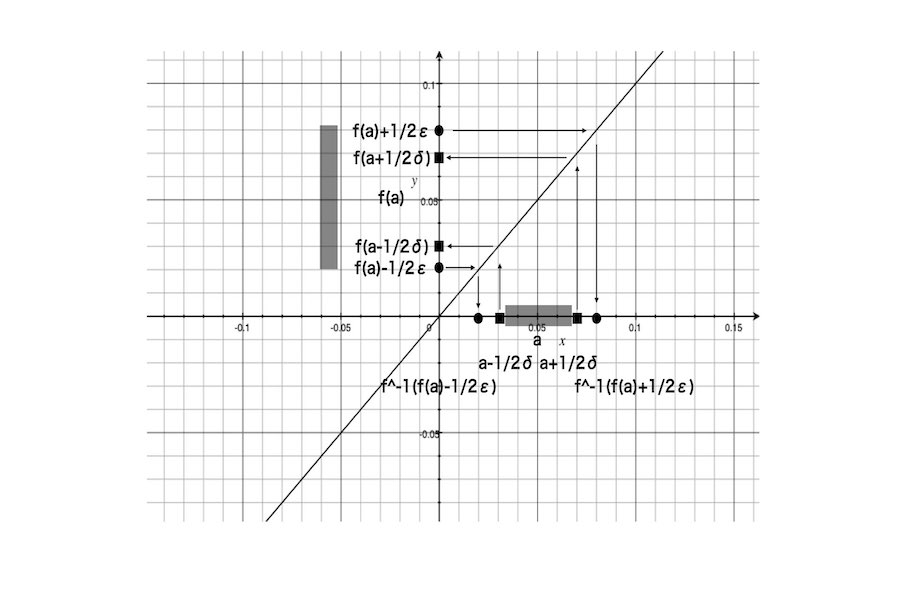
または、f^-1(f(a)+(1/2)ε<a-(1/2)δ<a<a+(1/2)δ<f^-1(f(a)+(1/2)ε)→f(a)-(1/2)ε<f(a-(1/2)δ<f(a)<f(a+(1/2)δ)<f(a)+(1/2)ε。筆者は上記では駄目であるのかを判定することができない。
2.0 関数の極限
2.1 定義
2.1(俺系統の認識) 任意の実数εに対して、ある実数δが存在する、かつ変数xとある定点aとの差の絶対値がその実数δよりも小さい,、かつその絶対値が0よりも大きいならば、関数値f(x)と極限値αとの差の絶対値が実数εよりも小さい。
0<|x-a|<δ→|f(x)-α|<ε。彼は関数の極限と関数の連続性の違いが何であるのかを理解できない。ここで、彼はy=x、ただし原点における値が1であるような関数f'(x)を考える。つまり、f(0)=1、y=x(x<0, x>0)を考える。
この時、この関数f'(x)は原点において連続でないが、極限値0を持つ可能性がある。なぜなら、0<|x-a|<δ→|f(x)-α|<εは成立するが、|x-a|<δ→|f(x)-f(a)|<εは成立しない。f(0)を取ると、f(0)=1になるので、εに対して、δを取れないので、イプシロン・デルタ論法が成立しない。しかし、極限値0を取ると、f(0)を考慮する必要がないので、上記の不等式が成立する。
また、直感的にも、関数f'(x)における極限値は0に近づけていくと、0になりそうに感じる。ただし、0クをxに代入すると、f'(0)=1が出てくる。
電飛
・イプシロンデルタ論法をわかりやすく丁寧に(数学の景色)
・イプシロンデルタ論法のデルタの求め方
・イプシロンデルタ論法(よびのり・youtube)
 |