無限級数 1 − 1 + 1 − 1 + … は次のように書き表すことができる。Σ(-1)^n。この級数はグランディ級数(グランディきゅうすう、英: Grandi’s series)と呼ばれることがある。グランディ級数という名前は、1703年にこの級数に関する議論において重要な貢献をした、イタリアの数学者であり哲学者である神父のルイージ・グイード・グランディ(英語版)に因む。グランディ級数は発散級数であり、通常の意味では和を持たない。その一方で、グランディ級数のチェザロ和は 1/2 となる。
https://ja.wikipedia.org/wiki/グランディ級数
以下では、俺は上記の級数を視覚化するつもりである。俺は$1-1+1-1+\dots$をMacのsoftware Grapherを使用して、この無限級数を解釈するつもりである。なお、真偽は不明である。なぜなら、俺は学者や数学教徒的な謙遜抜きに、俺は数学を理解していない。
1.0 グランディ級数
以下では、俺はグランディ級数を$$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)$$$$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)cos(kx)$$の二種類で表示するつもりである。一番目には、$cos(kx)$がない。二番目には、$cos(kx)$がある。杉山の電子場所(電飛)では、グランディ級数は$$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)$$表示される。
1.1 グランディ級数の視覚化〜cos(kx)なし〜
俺の視覚的予想1.1 $$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)=\frac{1}{2}$$ $$\sum_{k=1}^{∞}(-1)^{k-1}exp(-k\cdot 0)=0 \vee 1$$
以下では、俺は$$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)$$ をグラファーで表現していく。始めに、俺は$k=1$を視覚化してみよう。画像は「俺作成」である。なお、俺はグラファーによる数式の打ち間違いや機械の故障の可能性がないと断定しない。
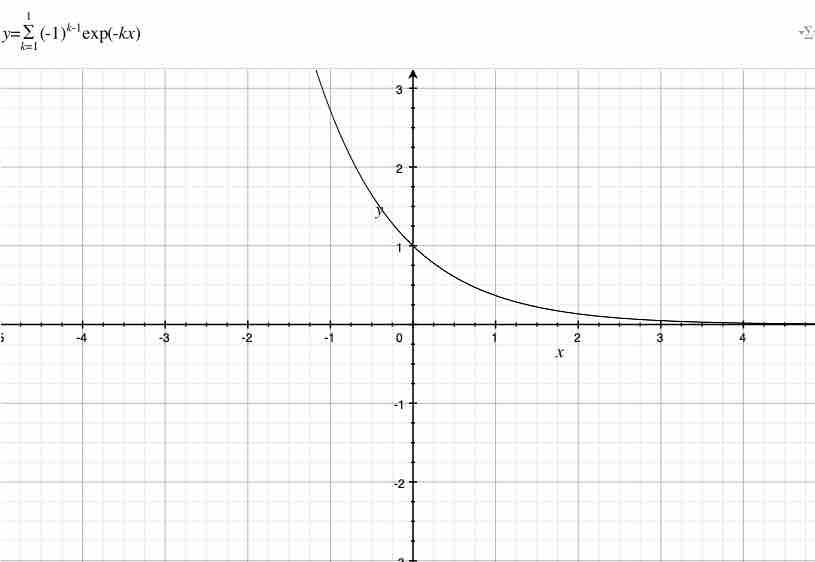
$k$が$1$のとき、$x=0$における杉山式の値は$1$である。計算は次である。$k$が$1$であるとき、杉山式は$$(-1)^{0}exp(-1x)$$である。
次に、俺は$0$を$x$に代入する。その時、俺は$$(-1)^{0}exp(-1\cdot 0)$$を獲得する。$exp(0)$は$0$である。従って、$x=0$における杉山式の値は$1$である。また、日常的な感覚でも、$1$と$-1$の総和$\sum_{k=1}^{1}$は$1=1$である。次に、俺は$k=2$を視覚化してみよう。
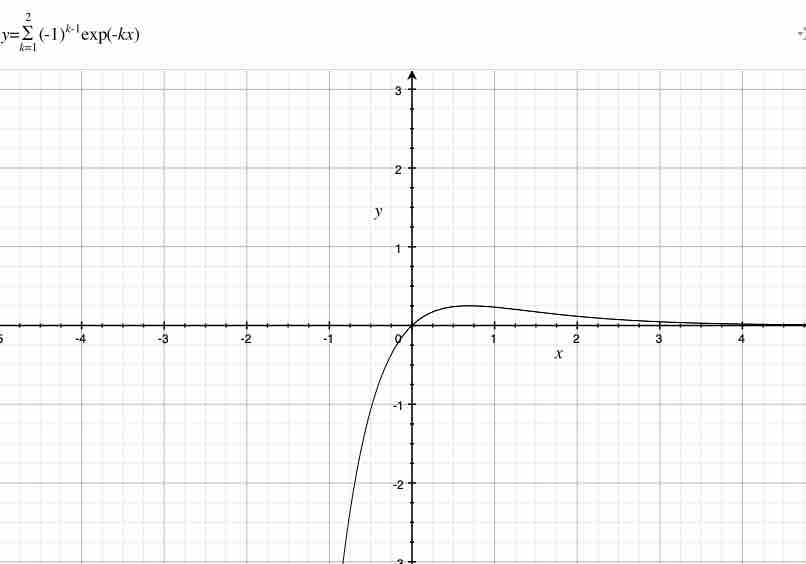
$k$が$2$のとき、$x=0$における値は$0$である。計算は次である。$k$が$2$であるとき、杉山式は$$(-1)^{0}exp(-1x)cos(1x)+(-1)^{1}exp(-2x)$$である。
次に、俺は$0$を$x$に代入する。その時、俺は$$(-1)^{0}exp(-1\cdot0)+(-1)^{1}exp(-2\cdot 0)$$を獲得する。従って、$x=0$における杉山式の値は$1+(-1)=0$である。また、日常的な感覚でも、$1$と$-1$の総和$\sum_{k=1}^{2}$は$1+(-1)=0$である。
同様に、俺は$k=3$や$k=4$を視覚化していく。$k=3$では、$1$が得られることが予想される。$k=4$では、$0$が得られることが予想される。次に、俺は$k=10$を取ってみる。俺は次の図を獲得する。
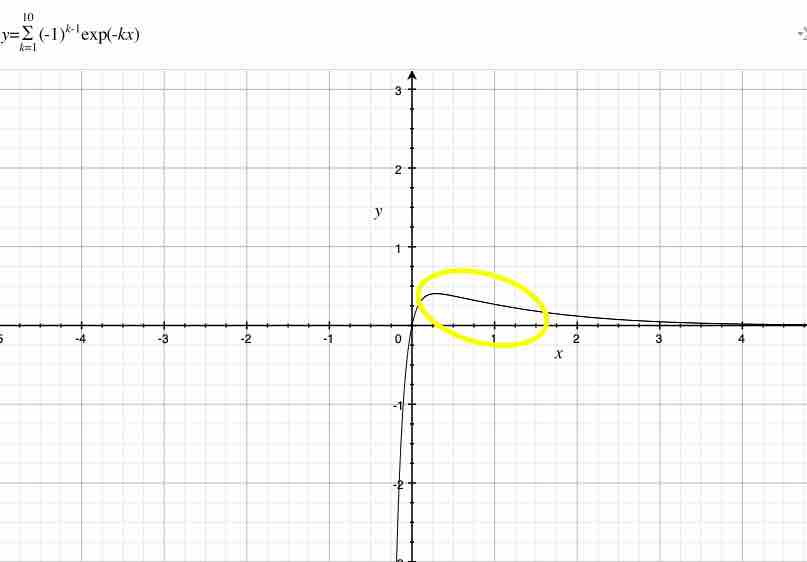
$k$が$10$のとき、$x=0$における値は$0$である。計算は次である。$k$が$10$であるとき、杉山式は$$(-1)^{0}exp(-1x)+(-1)^{1}exp(-2x)+\dots +(-1)^{9}exp(-10x)$$である。
次に、俺は$0$を$x$に代入する。その時、俺は$$(-1)^{0}exp(-1\cdot 0)+(-1)^{1}exp(-2\cdot 0)+\dots+(-1)^{9}exp(-10\cdot 0)$$を獲得する。従って、$x=0$における杉山式の値は$1+(-1)+\dots +(-1)=0$である。また、日常的な感覚でも、$1$と$-1$の総和$\sum_{k=1}^{10}$は$1+(-1)+…+(-1)=0$である。
ここで、俺は黄色の楕円に着目する。$x>0$における楕円の内部には、ある値が存在しているように見える。俺の予想として、もし俺が$k$を大きくするならば、この楕円の部分が$\frac{1}{2}$に近い値になるだろう。
次に、俺は$k=100$を取ってみる。
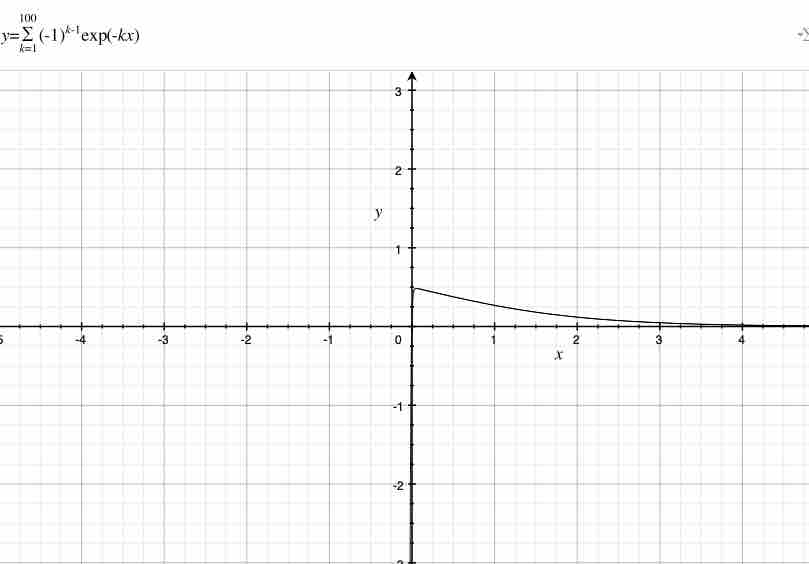
$k$が$100$のとき、$x=0$における値は$0$である。俺はその値を観察することはできない。$k$が100であるとき、杉山式は$$(-1)^{0}exp(-1\cdot 0)+(-1)^{1}exp(-2・0)+\dots +(-1)^{99}exp(-100x)$$である。
次に、俺は$0$を$x$に代入する。その時、俺は$$(-1)^{0}exp(-1\cdot 0)+(-1)^{1}\cdot exp(-2\cdot 0)+\dots +(-1)^{99}exp(-100\cdot 0)$$を獲得する。従って、$x=0$における杉山式の値は$1+(-1)+…+(-1)=0$である。また、日常的な感覚でも、$1$と$-1$の総和$\sum_{k=1}^{100}$は$1+(-1)+…+(-1)=0$である。
上記をみると、$x$が$0$に近い範囲では、杉山式は特定の値を取っているように見える。また、一つの山がある。俺が上記を拡大して、俺は次の図を獲得する。
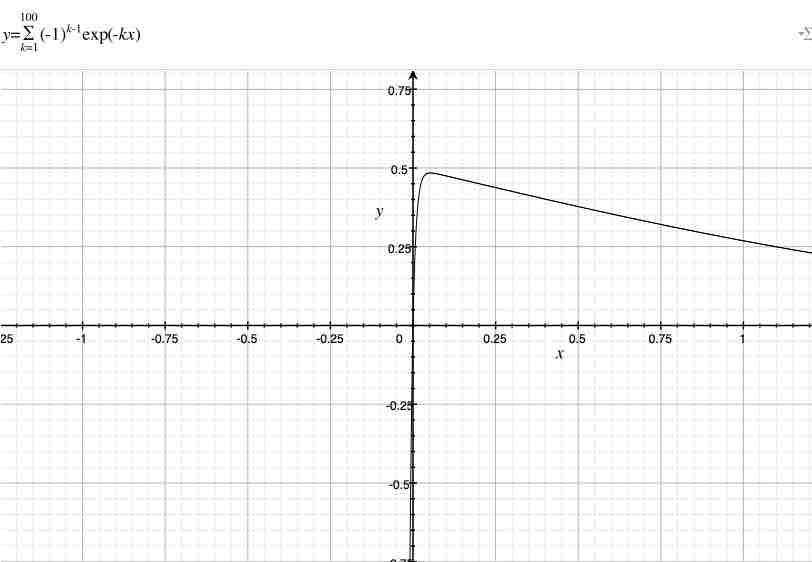
$x>0$における山がとる値は$\frac{1}{2}$であるように感じる。数学的な厳密性を捨てて、個人的な印象を提示すると、俺がkを無限にするとき、もし俺がxを正から0へと変化させるならば、その時、lim(x→+0)における杉山式の値は$\frac{1}{2}$にもなるように思える。当然、その時、1と-1の総和Σkは0、または1である。k=500も同様である。
kが無限のとき、x=0における値は1と-1の総和である。俺はその値を観察することはできない。kが無限であるとき、杉本式は$$(-1)^{0}exp(-1x)+(-1)^{1}exp(-2x)+\dots$$である。
次に、俺は0をxに代入する。その時、俺は$$(-1)^{0}exp(-1\cdot 0)+(-1)^{1}exp(-2\cdot 0)\dots$$を獲得する。従って、x=0における杉山式の値は1+(-1)+…=0、または1である。また、日常的な感覚でも、1と-1の総和Σkは1+(-1)+…=0、または1である。
ただし、kが無限のとき、もし俺が0をxに代入せずに、xを正から0へと変化させるならば、杉山式はlim(x→+0)における杉山式の値は$\frac{1}{2}$にもなるように思える。
2.0 グランディ級数の視覚化〜cos(kx)あり〜
2.1(俺の視覚的予想)
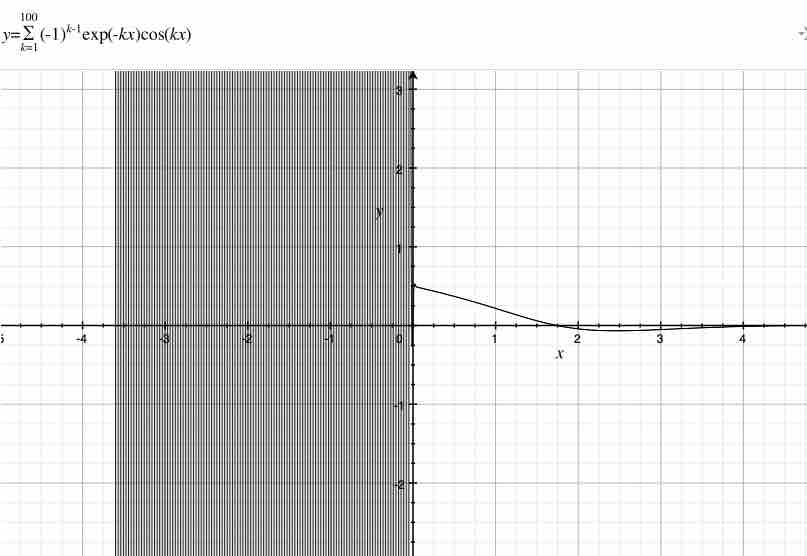
$$\lim_{+x \to +0}\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)cos(kx)=\frac{1}{2}$$ $$\sum_{k=1}^{∞}(-1)^{k-1}exp(-kx)cos(kx)=0 \vee1$$
上記は$cos(kx)$がある場合である。俺は上記と同様な操作を繰り返した。その結果、俺は上記のグラフを獲得した。



書き込み欄
学者的な謙遜を抜きにして、俺は数学を理解できない。だから、俺は上記の視覚化の真偽を判定できない。ただ、俺が英語圏を含む電街(インターネット)を検索したところ、俺の知る範囲では、誰も上記の視覚化を実行していなかった。そこで、俺は視覚化を実行した。
上記の視覚化は有用であるだろうか?個人的には、俺は教育などの分野において使えるのでないかと感じた。誰か、上記の視覚化が正しいのかを俺に “優しく” 教えて欲しい。また、上記の画像や動画は教育の分野において使用されることができるのかを知りたい。消去するのはもったいないように感じた。
なお、俺への話しかけは「タメ口」で良い。まとめると、俺の疑問は次になる。
質問①「上記の画像や動画における視覚化は正しいのか?」
質問②「上記の画像や動画は研究や教育で使用可能であるのか?」