自然数の総和（無限和）1+2+3+4+…が-1/12になる事の視覚化とその解釈について〜ゼータ関数ζ(-1)と1＋2＋3＋…＝-1/12〜

　自然数の総和1+2+3+4+…は無限∞である。しかし、自然数の総和1+2+3+4+…は-1/12にもなるらしい。正確には、”1+2+3+4+…”=-1/12であるらしいが、自然数を無限に足していくと、ある負の数が登場するのは奇妙である。特に、正の自然数を無限に足すと、負の数が登場するのは奇妙である。

　俺はこの違和感を解決するために、杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$を使用して、自然数の総和が無限と-1/12になることを同時に直感的に視覚化した。

　無限の場合、俺は無限級数1+2+3+4+…を次のように解釈した。

$\sum_{k=1}^{∞}kexp(-k \cdot 0)cos(k \cdot 0)＝∞$ $\tag{0.0.0}$

　-1/12の場合、俺はこの無限級数1+2+3+4+…を次のように解釈した。

$\lim_{x \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)=-\frac{1}{12}$ $\tag{0.0.1}$

　俺はこの式を杉山式と呼ぶ。上記の式は杉山に依存する（関連）。

１章　自然数の無限和を視覚化しよう！〜1+2+3+…=-1/12の視覚化〜

　ここでは、俺は自然数の無限和を視覚化する。俺はマックのやわもの「グラファー」を使用した。このとき、俺は自然数の無限和が無限になることと自然数の無限和が-1/12になることを同時に視覚化することができた。

１節　視覚的な現象を作ろう！

視覚的な予想1.1
$\sum_{k=1}^{∞}kexp(-k \cdot 0)cos(k \cdot 0)＝∞$ $\tag{1.1.1}$
$\lim_{x \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)=-\frac{1}{12}$　$\tag{1.1.2}$

　俺は$1+2+3+4+ \dots$が無限$∞$と$-\frac{1}{12}$になることを杉山式(1.1.1)と(1.1.2)で同時に視覚化する。$x=0$では、$1+2+3+4+ \dots=∞$が視覚的に観察された。そこでは、自然数の和が$x=0$でy軸方向に大きくなっていった。$x>0$では、$1+2+3+4+ \dots=-\frac{1}{12}$が視覚的に観察された。そこでは、$-\frac{1}{12}$が$x>0$から$x=0$へと近づいていった。

k=1のとき

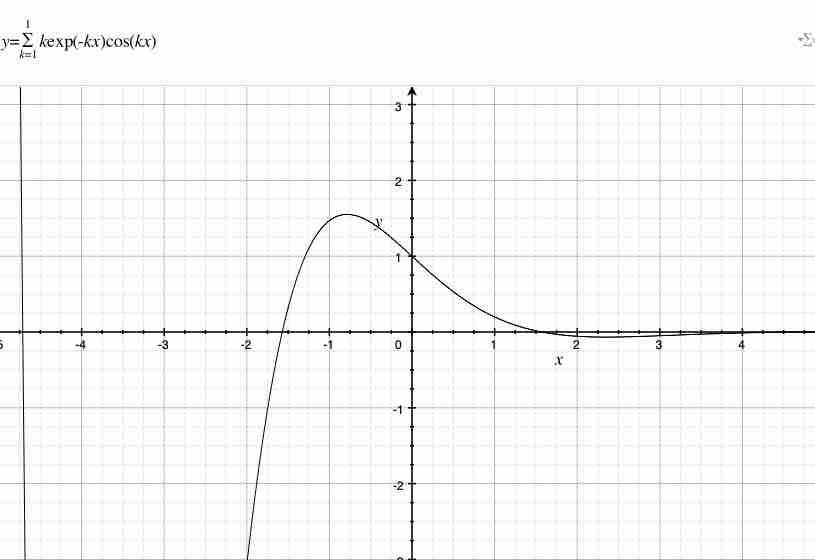
　始めに、$k=1$のときの杉山式の様子を見てみよう。$k$が$1$のとき、図1.1によると、$x=0$における杉山式の値は$1$である。

　$k$が$1$であるとき、杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$は次である。

$\sum_{k=1}^{1}kexp(-k \cdot x)cos(k \cdot x)$
$＝1exp(-1x)cos(1x)$ $\tag{1.1.3}$

　$0$を杉山式の$x$に代入して、$k=1$とすると、俺は次を獲得する。

$\sum_{k=1}^{1}kexp(-k \cdot 0)cos(k \cdot 0)$
$＝1exp(-1 \cdot 0)cos(1 \cdot 0)=1$
$\tag{1.1.4}$

　なお、$exp(0)$及び$cos(0)$は$1$である。従って、$x=0$における杉山式の値は$1$である。また、日常的な感覚でも、自然数の総和$\sum_{k=1}^{1}k$は$1＝1$である。

　極限を使用した場合は次である。

$\lim_{x \to +0}\sum_{k=1}^{1}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}1exp(-1x)cos(1x)=1$
$\tag{1.1.5}$

　視覚的には、上記の図において、$x$を$x>0$から$x=0$に移動させる。すると、$x=0$で、$x=1$になる。

k=2のとき

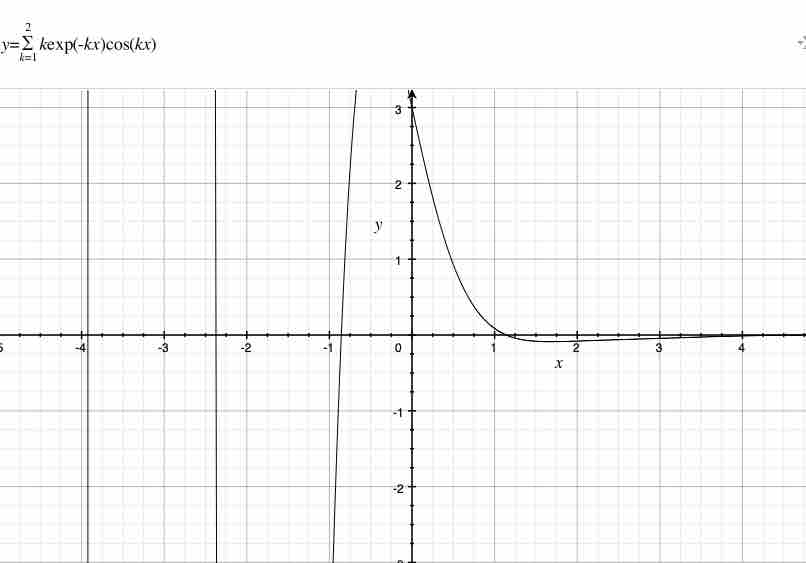
　次に、$k=2$のときの杉山式の様子を見てみよう。$k$が$2$のとき、図1.2によると、$x=0$における杉山式の値は$3$である。

　$k$が$2$であるとき、杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$は次である。

$\sum_{k=1}^{2}kexp(-k \cdot x)cos(k \cdot x)$
$＝1exp(-1x)cos(1x)+2exp(-2x)cos(2x)$ $\tag{1.1.6}$

　$0$を杉山式の$x$に代入して、$k=2$とすると、俺は次を獲得する。

$\sum_{k=1}^{2}kexp(-k \cdot 0)cos(k \cdot 0)$
$＝1exp(-1 \cdot 0)cos(1 \cdot 0)+2exp(-2 \cdot 0)cos(2 \cdot 0)$
$=1+2=3$
$\tag{1.1.7}$

　$x=0$における杉山式の値は$1+2=3$である。また、日常的な感覚でも、自然数の総和$\sum_{k=1}^{2}k$は$1+2=3$である。同様に、俺は$k=3$や$k=4$を視覚化する。ただし、その様子を省略する。

　極限を使用した場合は次である。

$\lim_{x \to +0}\sum_{k=1}^{2}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}(1exp(-1x)cos(1x)+2exp(-2 \cdot 0)cos(2 \cdot 0))$
$=3$ $\tag{1.1.8}$

　視覚的には、上記の図において、$x$を$x>0$から$x=0$に移動させる。すると、$x=0$で、$x=3$になる。

k=10のとき

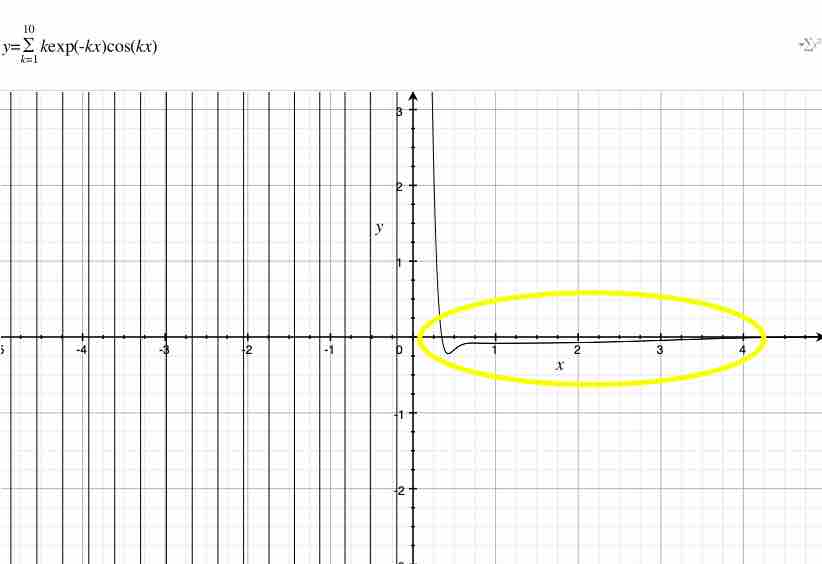
図1.3　k=10 ここで、筆者は黄色の楕円に着目する。$x>0$における楕円の内部には、ある値が存在しているように見える。筆者の予想として、もし筆者が$k$を大きくするならば、この楕円の部分が$-\frac{1}{12}$に近い値になる。

　さらに、$k=10$のときの杉山式の様子を見てみよう。$k$が$10$のとき、図1.3によると、$x=0$における杉山式の値は$55$である。俺は55をその図から見ることができない。

　$k$が$10$であるとき、杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$は次である。

$\sum_{k=1}^{10}kexp(-k \cdot x)cos(k \cdot x)$
$=1exp(-1x)cos(1x)+…+10exp(-10x)cos(10x)$ $\tag{1.1.9}$

　$0$を杉山式の$x$に代入して、$k=10$とすると、俺は次を獲得する。

$\sum_{k=1}^{10}kexp(-k \cdot 0)cos(k \cdot 0)$
$＝1exp(-1\cdot 0)cos(1\cdot 0)+…+10exp(-10\cdot 0)cos(10\cdot 0)$
$＝1+…+10=55$ $\tag{1.1.10}$

　$x=0$における杉山式の値は$1+…+10=55$である。また、日常的な感覚でも、自然数の総和$\sum_{k=1}^{10}$は$1+…+10＝55$である。ここで、俺は黄色の楕円に着目する。$x>0$における楕円の内部には、ある値が存在しているように見える。俺の予想として、もし俺が$k$を大きくするならば、この楕円の部分が$-\frac{1}{12}$に近い値になる。

　極限を使用した場合は次である。

$\lim_{x \to +0}\sum_{k=1}^{10}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}(1exp(-1x)cos(1x)+…+10exp(-10 \cdot 0)cos(10 \cdot 0))$
$=55$ $\tag{1.1.11}$

　視覚的には、上記の図において、$x$を$x>0$から$x=0$に移動させる。すると、$x=0$で、$x=55$になる。

k=100のとき

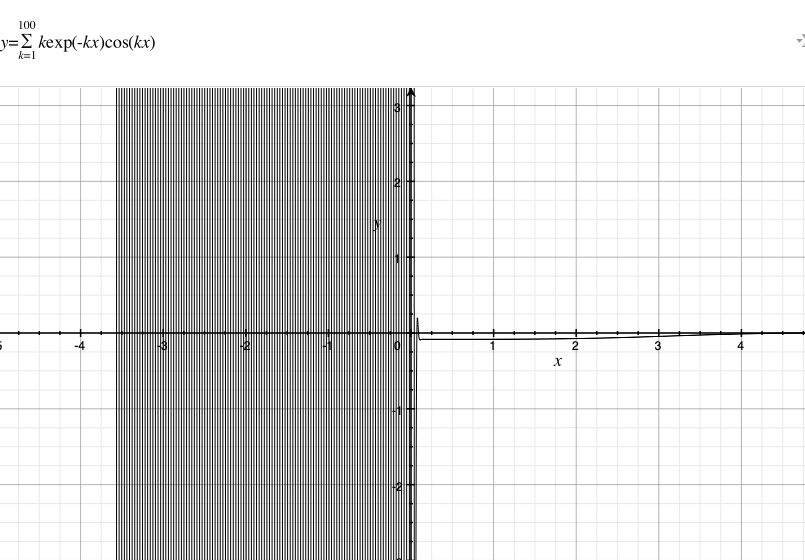
　　次に、$k=100$のときの杉山式の様子を見てみよう。$k$が$100$のとき、図1.4によると、$x=0$における杉山式の値は$5050$である。当然、俺はその値を観察することはできない。

　　$k$が$100$であるとき、杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$は次である。

$\sum_{k=1}^{100}kexp(-k \cdot 0)cos(k \cdot 0)$
$＝1exp(-1x)cos(1x)+…+100exp(-100x)cos(100x)$ $\tag{1.1.12}$

　$0$を杉山式の$x$に代入して、$k=100$とすると、俺は次を獲得する。

$\sum_{k=1}^{100}kexp(-k \cdot 0)cos(k \cdot 0)$
$＝5050$ $tag{1.1.13}$

　$x=0$における杉山式の値は$1+…+100=5050$である。また、日常的な感覚でも、自然数の総和$\sum_{k=1}^{100}$は$1+…+100＝5050$である。上記をみると、$x$が$0$に近い範囲では、杉本式は特定の値を取っているように見える。また、一つの山がある。俺が上記の図を拡大して、俺は次の図1.5を獲得する。

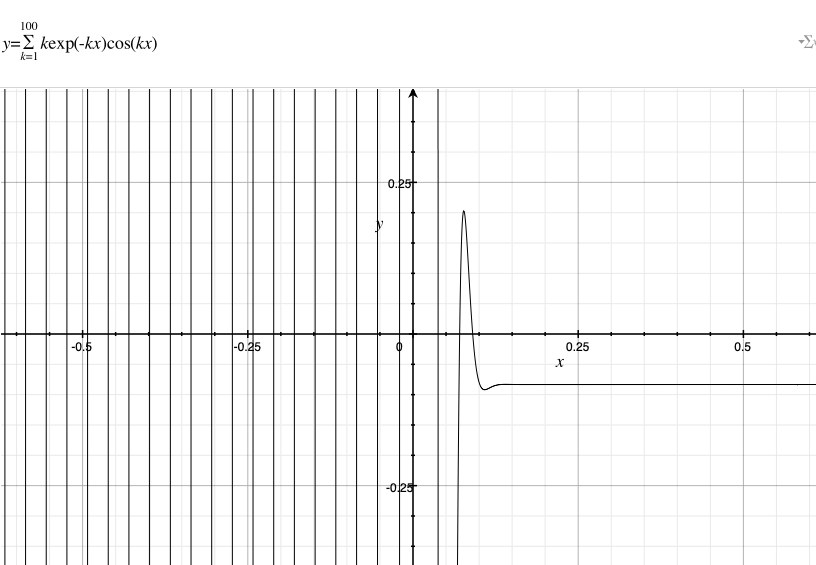
　$x>0$における直線をとる値は$-\frac{1}{12}$であるように見える。$y=-\frac{1}{12}$を導入すると、俺は次の図1.6を獲得する。

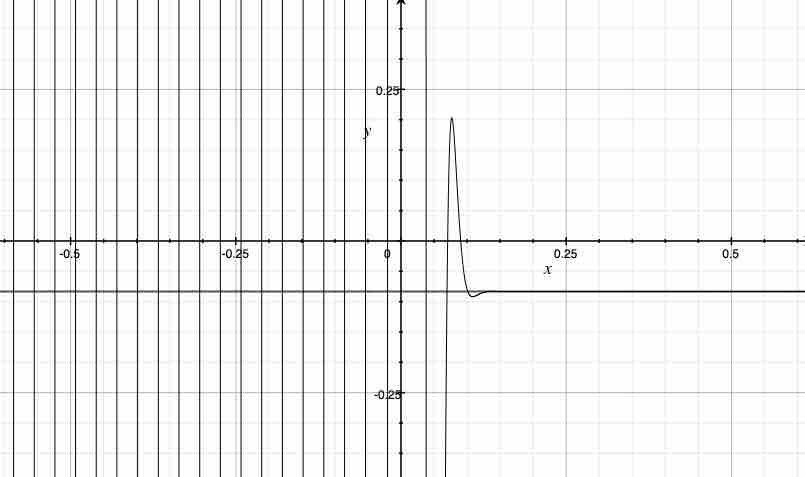
　上記の直線は$y=-\frac{1}{12}$である。$x>0$における直線をとる値は約$y=-\frac{1}{12}$である。数学的な厳密性を捨てて、個人的な印象を提示すると、俺が$k$を無限にするとき、もし俺が$x$を正から$0$へと変化させるならば、その時、$\lim_{+x \to +0}$における杉山式の値は$y=-\frac{1}{12}$にもなるように思える。その時、$x=0$における自然数の総和$\sum_{k=1}^{∞}$は無限である。$k=500$も同様である。

　極限を使用した場合は次である。

$\lim_{x \to +0}\sum_{k=1}^{100}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}(1exp(-1x)cos(1x)+…+100exp(-100 \cdot 0)cos(100 \cdot 0))$
$=5050$ $\tag{1.1.14}$

　視覚的には、上記の図において、$x$を$x>0$から$x=0$に移動させる。すると、$x=0$で、$x=5050$になる。

k=無限

　$k$が無限のとき、$x=0$における値は自然数の総和$∞$である。俺はその値を観察することはできない。$k$が無限であるとき、杉山式は次である。

$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$
$=1exp(-1x)cos(1x)+2exp(-2x)cos(2x)+…$ $\tag{1.1.15}$

　次に、それが可能な操作であるならば、筆者は$0$を$x$に代入する。その時、俺は次を獲得する。

$1exp(-1 \cdot 0)cos(1 \cdot 0)+2exp(-2 \cdot 0)cos(2 \cdot 0)…$
$=1+2+…=∞$ $\tag{1.1.16}$

　$x=0$における杉山式の値は$1+2+…=∞$である。また、日常的な感覚でも、自然数の総和$\sum_{k=1}^{∞}$は$1+2+…＝∞$である。

　ただし、$k$が無限のとき、もし俺が$0$を$x$に代入せずに、$x$を正から$0$へと変化させるならば、杉山式は$\lim_{+x \to +0}$における杉山式の値は$-\frac{1}{12}$にもなるように思える。当然、上記の図によると、$-\frac{1}{12}$を取らない山がある。だから、もしこの山が消失しないならば、たとえ筆者が$x$を正から$0$へと変化させるとしても、$\lim_{+x \to +0}$における杉山式の値は$-\frac{1}{12}$にもならないように思える。だから、上記を主張するためには、この山の除去や山の解釈が必要である。

　極限を使用した場合は次である。

$\lim_{x \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}(1exp(-1x)cos(1x)+…)=∞$ $\tag{1.1.17}$

　視覚的には、上記の図において、$x$を$x>0$から$x=0$に移動させる。すると、$x=0$で、$x=∞$になる。

$\lim_{x \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)$
$=\lim_{x \to +0}(1exp(-1x)cos(1x)+…)=-\frac{1}{12}$ $\tag{1.1.18}$

　上記の極限が普通の極限操作であるのかは不明である。しかし、上記の図を見ると、$k=∞$では、$-\frac{1}{12}$が$x=0$において生じるように思える。

２節　解釈しよう！

【視覚的な解釈1.2】
①　$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$の$x$が$0$である時、$1+2+3+4+…$が$∞$になる。視覚的には、杉山式のグラフにおいて、$x=0$における$y$軸の値が無限$∞$へと発散する。

②　$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$ が $\lim_{x \to +0}$ である時、 $1+2+3+4+…$ が $-\frac{1}{12}$ になる。視覚的には、杉山式のグラフにおいて、$x=0$ における $y$ 軸の値 $-\frac{1}{12}$ が $x>0$ から $0$ へと収束するように見える。　

③　$\sum_{k=1}^{k}kexp(-kx)cos(kx)$ が $\lim_{x \to +0}$ である時、その値は$\sum_{k=1}^{k}kexp(-k \cdot 0)cos(k \cdot 0)$ に一致する。無限の場合でも、その値は∞と $-\frac{1}{12}$ になる。

　直感的には、自然数の総和は無限である。つまり、$1＋2＋3＋4+…$は無限$∞$である。この視覚的な解釈は$x=0$における$y$の値が$1, 1+2, 1+2+3+, …$のように$x=0$で大きくなることである。$1+2+3+4+…$が$\lim_{+x \to +0}(1exp(-1x)cos(1x)+2exp(-2x)cos(2x)+3exp(-3x)cos(3x)+4exp(-4x)cos(4x)+…)$のとき、$1+2+3+4+…$は$-\frac{1}{12}$である可能性がある。

　上記の無限級数では、無限級数におけるそれぞれの数を$kexp(-kx)cos(kx)$の$x=0$における値と解釈することができる可能性がある。その時、その級数は$-\frac{1}{12}$になるかもしれない。一方、級数におけるそれぞれの数を自然数と解釈する時、その級数は無限へと発散する。上記の図では、上記の無限級数は発散する、かつ$-\frac{1}{12}$になるかもしれない。個人的な印象では、上記の級数は収束しているのでなく、直感通りに発散しているように見える。

　一般的に、関数はある変数に対して一つの値を取っているように見える。しかし、上記では、x=における値は$∞$と$x>0$から$x=0$への極限値$-\frac{1}{12}$である。つまり、杉山式は$x=0$において二つの値を取っているように見える。

2乗和と3乗和

　以下では、俺はその他の無限級数$1^n+2^n+3^n+4^n$を提示する。無限級数には、$1^2+2^2+3^2+4^2+…$と$1^3+2^3+3^3+4^3+…$がある。これらのどれもが発散するように思える。けれども、俺が無限級数のそれぞれの項をある関数における$x=0$の値と解釈する時、俺はこの無限級数に対する異なる解釈を獲得する。

2乗和

【視覚的な予想2.1】　
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^2exp(-kx√3)cos(kx)=0$$ $$\sum_{k=1}^{∞}k^2exp(-k \cdot 0 \cdot √3)cos(k \cdot 0)＝∞$$

　以下では、俺はこの無限級数を$\lim_{+x \to +0}\sum_{k=1}^{∞}k^2exp(-kx√3)cos(kx)$と解釈する。$1^2+2^2+3^2+4^2+…$は$\lim_{+x \to +0}lim(1^2exp(-1x√3)cos(1x)+2^2exp(-2x√3)cos(2x)+3^2exp(-3x√3)cos(3x)+…)$である。俺はこの数式を杉山の電子場所（電飛）で発見した。そこで、俺はこの数式を杉本式2と便宜的に呼ぶ。

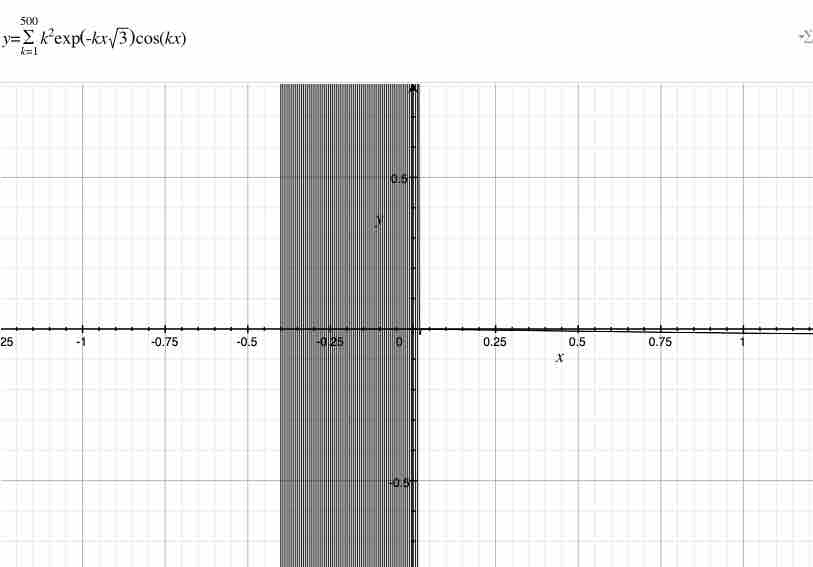
　この級数は$0$になるらしい。見づらいが、$x>0$から$x=0$へにかけて、杉山式2は$0$に近づいていっているように見える。拡大すると、俺は次を獲得する。

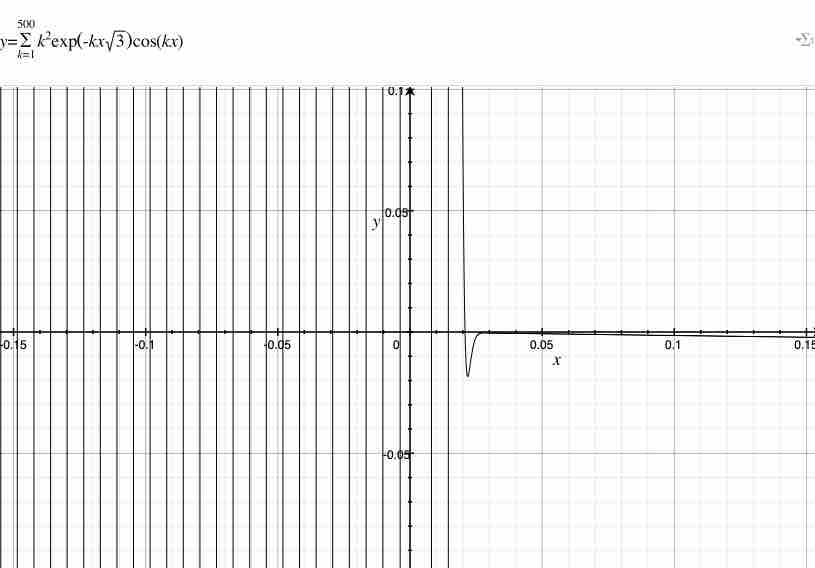
上記を見ると、俺は$k$が無限の時、もし俺が$x$を$x>0$から$x=0$へと変化させるならば、俺は杉山式2の値が$0$に収束するように感じる。考え方は上記と同様であるので、省略する。

3乗和

　【視覚的な予想2.2】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^3exp(-kx(1+√2))cos(kx)=\frac{1}{120}$$ $$\sum_{k=1}^{∞}k^3exp(-k \cdot 0 \cdot (1+√2))cos(k \cdot 0)＝∞$$

以下では、俺はこの無限級数を$\lim_{+x \to +0}\sum_{k=1}^{∞}k^3exp(-kx(1+√2))cos(kx)$と解釈する。$1^3+2^3+3^3+4^3+…$は$\lim_{+x \to +0}(1^3exp(-1x(1+√2))cos(1x)+2^3exp(-2x(1+√2))cos(2x)+3^3exp(-3x(1+√2))cos(3x)+…)$である。俺はこの数式を杉山の電子場所（電飛）で発見した。そこで、俺はこの数式を杉本式3と便宜的に呼ぶ。また、

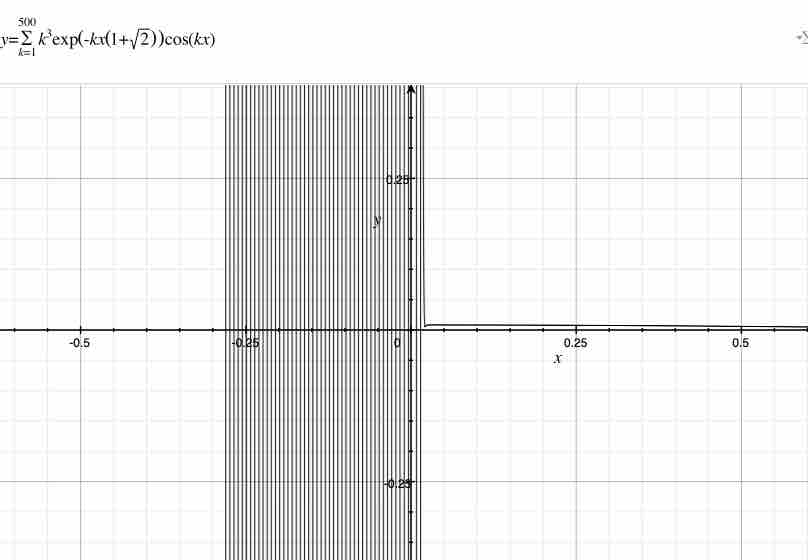
　この級数は$\frac{1}{120}$になるらしい。見づらいが、$x>0$から$x=0$へにかけて、杉山式3は$\frac{1}{120}$に近づいていっているように見える。拡大すると、俺は次を獲得する。なお、俺は$y=\frac{1}{120}$を導入した。

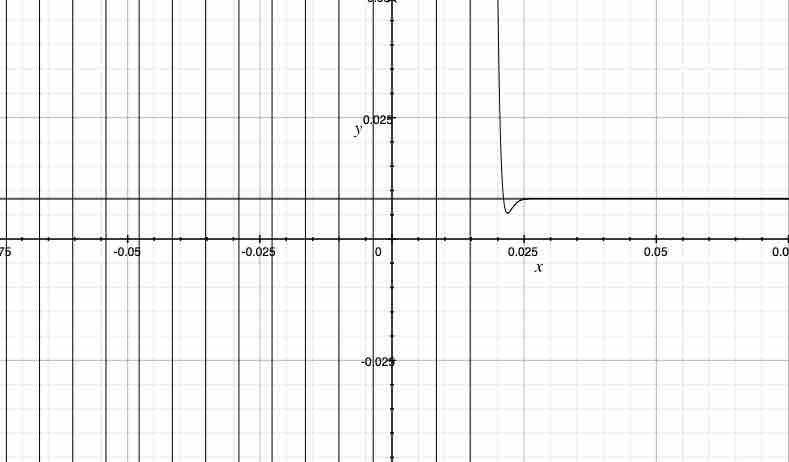
上記を見ると、俺は$k$が無限の時、もし俺が$x$を$x>0$から$x=0$へと変化させるならば、俺は杉山式3の値が$\frac{1}{120}$に収束するように感じる。また、$0$付近（$x$が$0.023$よりも大きい）の杉本式3の値は$y=\frac{1}{120}$に一致する。考え方は上記と同様であるので、省略する。

-2乗和と-3乗和とその他の-乗和

【拡張された杉山式】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{n}exp(-kxcot(\frac{π}{2n+2}))cos(kx)$$

以下では、筆者はその他の無限級数$1^n+2^n+3^n+4^n$を提示する。無限級数には、$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}…$と$\frac{1}{1^3}+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}……$と$\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}……$がある。これらのどれもが発散するように思える。けれども、筆者が無限級数のそれぞれの項をある関数における$x=0$の値と解釈する時、筆者はこの無限級数に対する異なる解釈を獲得する。同様に、筆者は上記の拡張された杉山式を使用する。俺は$n$に$n≦-2$の数を代入する。

-2乗和

　【視覚的な予想3.1】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2}))cos(kx)=\frac{π^2}{6}$$ $$\sum_{k=1}^{∞}k^{-2}exp(-k \cdot 0 \cdot cot(\frac{π}{-2}))cos(k \cdot 0)=\frac{π^2}{6}$$

　$n=-2$であるとき、$1^n+2^n+3^n+4^n+…$は$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}…$になる。杉山式によると、$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}…$は$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2})cos(kx)$である。$k=100$の時、俺は次の図を獲得した。

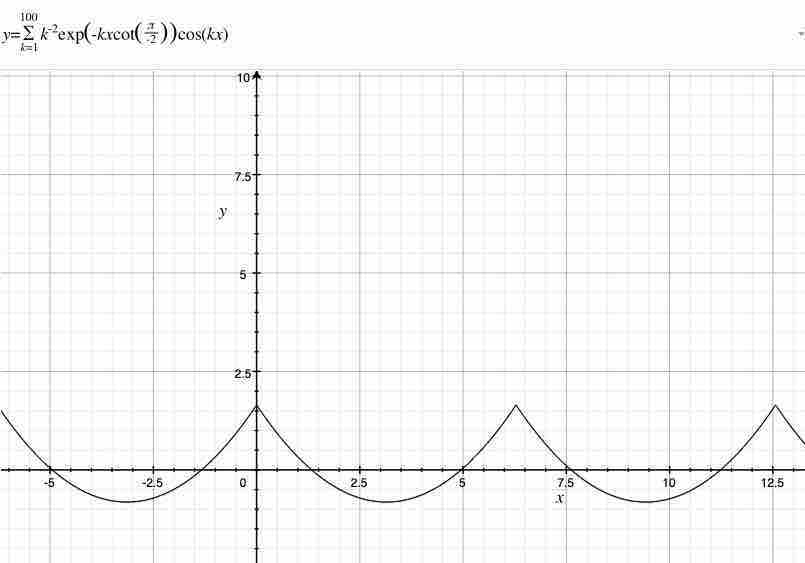
上記は$0≦n$の時と非常に異なるグラフの形である。俺は$y=\frac{π^2}{6}$を導入する時、俺は次の図を獲得する。

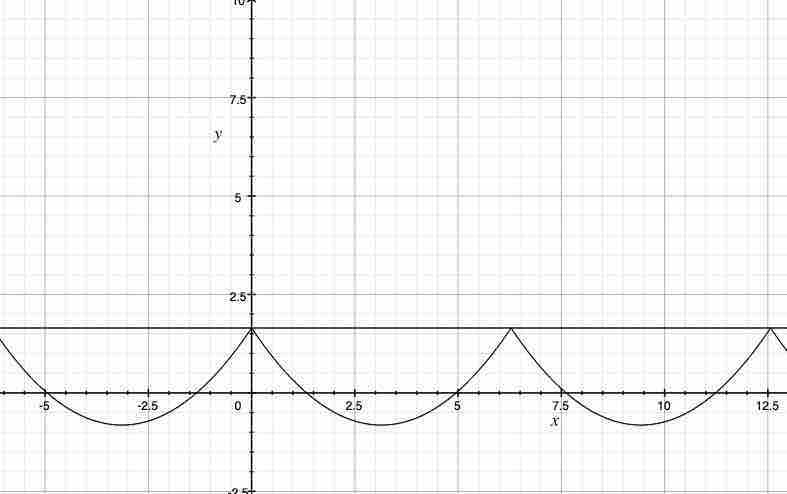
さらに拡大すると、俺は次の図を獲得する。

　俺が$k$を無限に近づけた時、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2}))cos(kx)$は$\frac{π^2}{6}$に収束しそうである。ただし、$0≦n$のとき、正確には、$1≦n$の時と異なり、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2}))cos(kx)$は$x=0$上で収束している。

それに対して、$0≦n$のとき、正確には、$1≦n$の時では、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2}))cos(kx)$はx=0で発散して、$x>0$から$0$への収束値を持った。ここでは、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-2}exp(-kxcot(\frac{π}{-2}))cos(kx)$は$x=0$上での収束値（$\frac{π^2}{6}$）を持つ一方、$x>0$から$0$への収束値を持っていない。

-3乗和

　【視覚的な予想3.2】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx)=1.20205…$$ $$\sum_{k=1}^{∞}k^{-3}exp(-k \cdot 0 \cdot cot(\frac{π}{-4}))cos(k \cdot 0)=1.20205…$$

　$n=-3$であるとき、$1^n+2^n+3^n+4^n+…$は$\frac{1}{1^3}+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}…$になる。杉山式によると、$\frac{1}{1^3}+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}…$は$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx)$である。k=100の時、俺は次の図を獲得した。

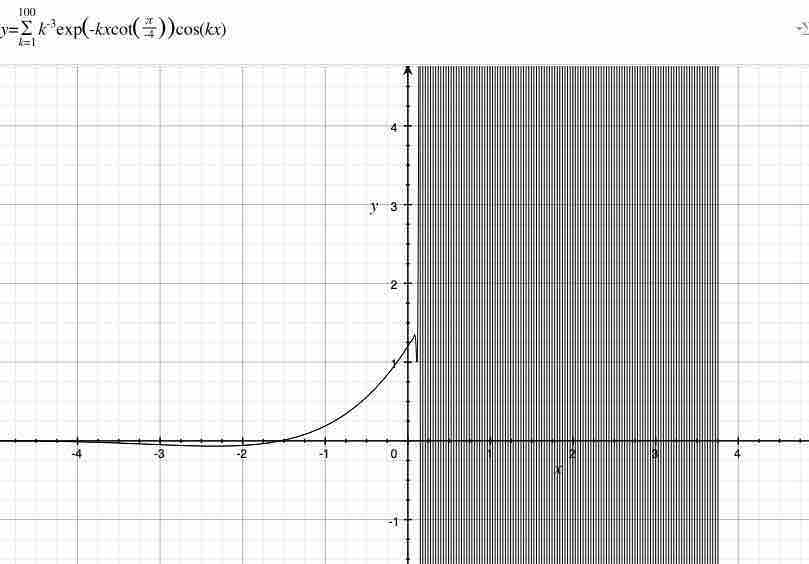
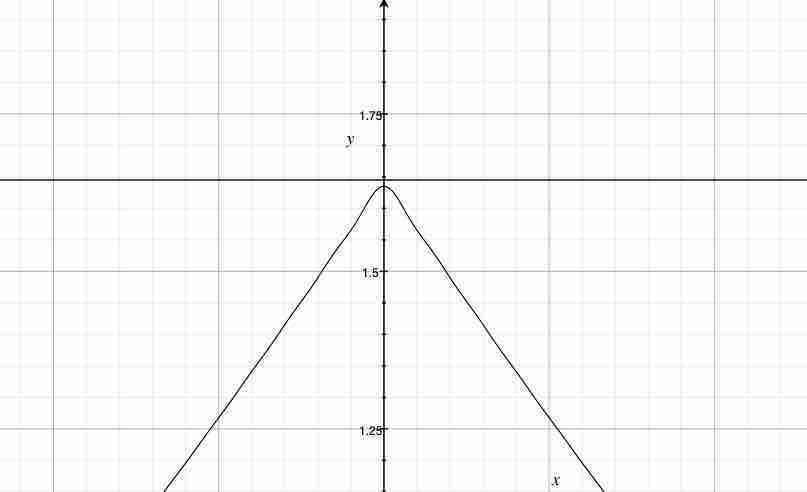
上記は$0≦n$の時と非常に異なるグラフの形である。俺は$y=1.20205$を導入する時、俺は次の図を獲得する。

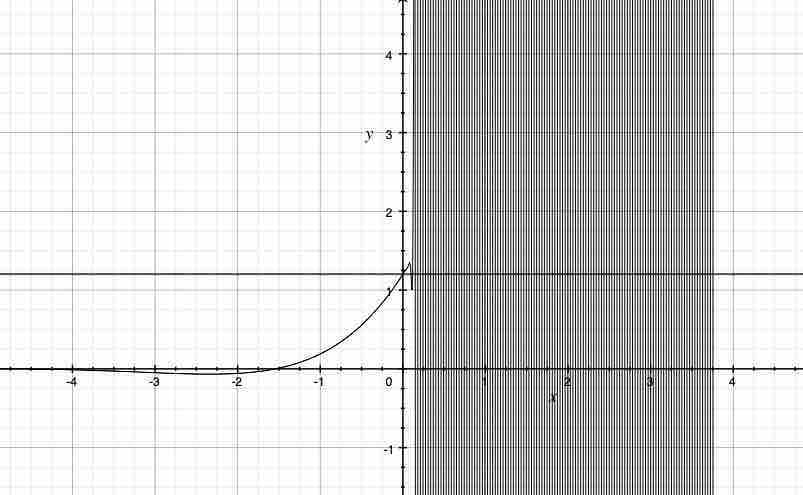
さらに拡大すると、俺は次の図を獲得する。

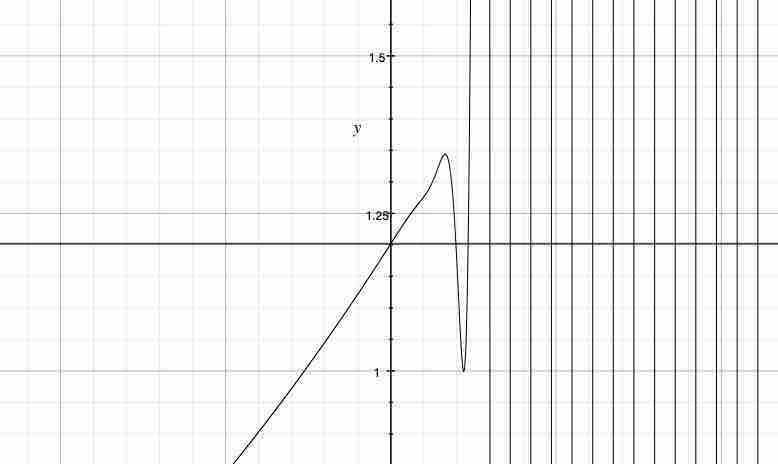
　俺が$k$を無限に近づけた時、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx)=1.20205…$に収束しそうである。ただし、$0≦n$のとき、正確には、$1≦n$の時と異なり、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx)=1.20205…$は$x=0$上で収束している。

それに対して、$0≦n$のとき、正確には、$1≦n$の時では、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx)$はx=0で発散して、$x>$0$から0$への収束値？を持った。ここでは、$\lim_{+x \to +0}\sum_{k=1}^{∞}k^{-3}exp(-kxcot(\frac{π}{-4}))cos(kx).$は$x=0$上での収束値（$1.20205…$）を持つ一方、$x>0$から$0$への収束値？を持っていない。

n≦-4の場合

　以下では、俺は$n≦-4$の時の杉山式を視覚化する。

【視覚的な予想3.3】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{-4}exp(-kxcot(\frac{π}{-6}))cos(kx)=\frac{π^4}{90}$$ $$\sum_{k=1}^{∞}k^{-4}exp(-k \cdot 0 \cdot cot(\frac{π}{-6}))cos(k \cdot 0)=\frac{π^4}{90}$$

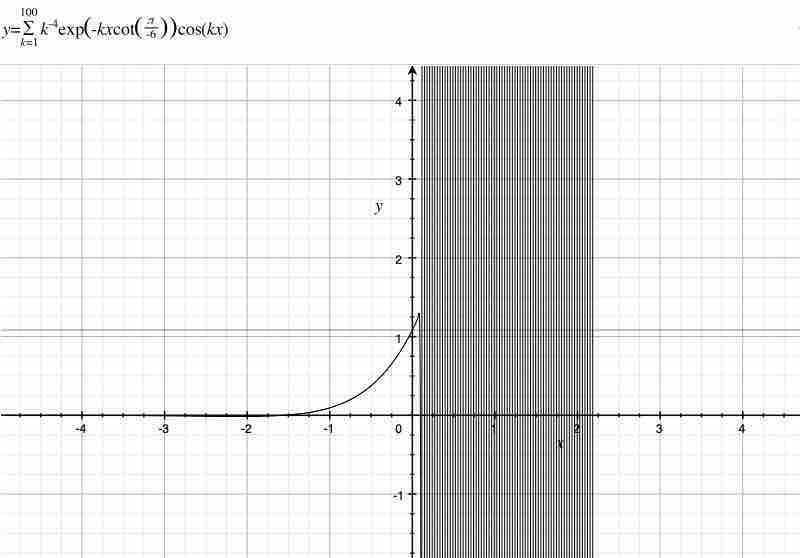
$y=1$の上の薄い直線が$y=\frac{π^4}{90}$である。俺は上記の図の拡大を省略する。

【視覚的な予想3.4】
$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{-5}exp(-kxcot(\frac{π}{-8}))cos(kx)=1.03692…$$ $$\sum_{k=1}^{∞}k^{-5}exp(-k \cdot 0 \cdot cot(\frac{π}{-8}))cos(k \cdot 0)=1.03692…$$

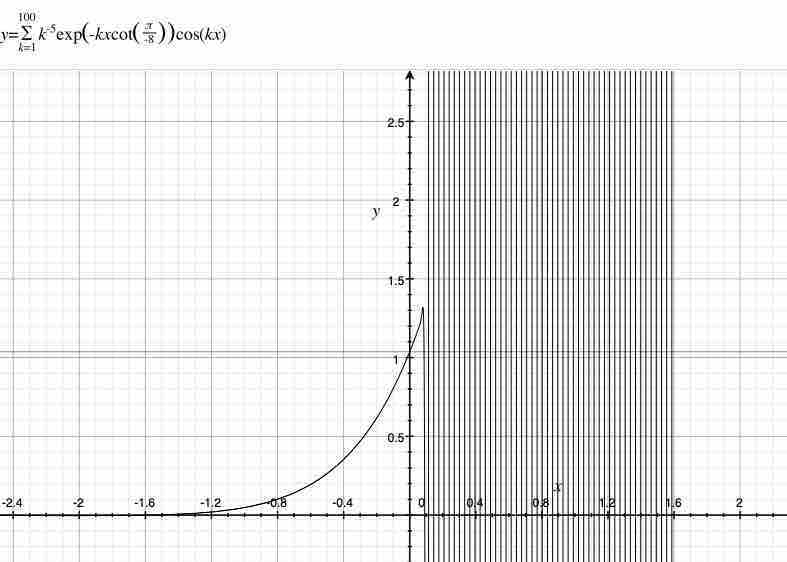
$y=1$の上の薄い直線が$y=1.03692$である。俺は上記の図の拡大を省略する。

筆者の行為

以上で、筆者は自然数の総和の視覚化を終えた。ここで、彼は彼自身の行為を簡単にまとめる。彼は彼が何をやったのかを下記でまとめる。数式それ自体は杉山に依存する。また、上記の視覚化が数学的に正しいのか、または本当に視覚化されているのかは不明である。

同時の視覚化

【筆者系統の認識】
筆者は1+2+3+4+…=∞と1+2+3+4+…=-1/2を同時に視覚化した。

筆者は杉山式を杉山と異なる方法で視覚化した。その結果、彼は無限級数において収束値がx>0からx=0へと近づいて行く様子を獲得した。同時に、彼は無限級数がx=0で感覚通りに発散することも視覚化した。

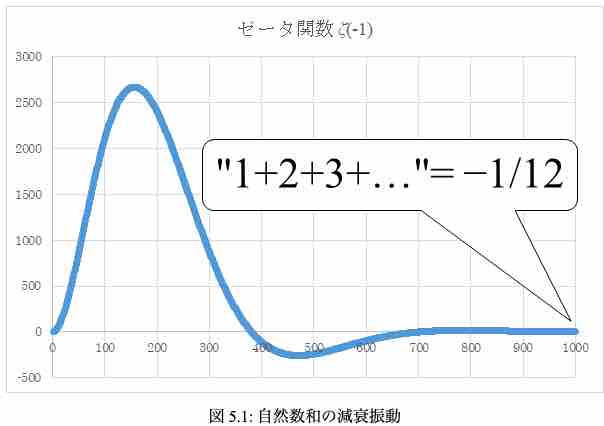
右の図にあるように、杉山はnを横軸にとり、yを縦軸に取った。そして、彼はnを大きくすると、yが大きなk（項数）において-1/12になることを視覚化した。

それに対して、筆者はxを横軸に取り、yを縦軸に取った。そして、それぞれのnに対して、俺はkを大きくしていった。それぞれのkは一枚のグラフ（図）に対応する。

その結果、筆者は無限級数において収束値、例えば-1/12がx>0からx=0へと近づいて行く様子を獲得した。同時に、俺は1+2+3+…がx=0で感覚通りに発散する視覚化も同じ一枚のグラフの中で獲得した。

杉山の視覚化では、1+2+3+…が無限になり、かつ-1/12になることを視覚化できていない。一方、上記の視覚化では、筆者は1+2+3+…が無限になり、かつ-1/12になることを視覚化した。

非常に直感的な視覚化

【筆者系統の認識】
筆者はある種の無限級数が特定の値、例えば-1/12や0や1/120を取ることを非常に直感的に視覚化することができた。

1+2+3+…が-1/12になることを証明するためには、複素数や解析接続の考えが必要であるらしい。しかし、筆者の図示では、彼は1+2+3+…が-1/12と1+2+3+…が無限になることを直感的に視覚化することができるようになった。つまり、1+2+3+…が無限になるのは、x=0上でのyの値が無限へと大きくなることであり、1+2+3+…が-1/12になるのは、x>0からx=0へとy=-1/12が近づいていくことである。

解釈

【筆者系統の認識】
筆者は杉山式を視覚的に解釈して、1+2+3+…が-1/12と1+2+3+…が無限になることを視覚的に解釈した。

杉山式のグラフでは、杉山式が-1/12になることのみが視覚化されている。杉山の図示では、杉山は杉山式が-1/12を取ることを確認した。それに対して、筆者の図示では、筆者は1+2+3+…が-1/12なることと1+2+3+…が無限になることを同時に視覚的に解釈した。

筆者は1+2+3+…が-1/12なるのは-1/12がx>0からx=0へと近づいていった結果であると視覚的に解釈した。彼は1+2+3+…が-1/12なるのは無限がx=0で無限大へと発散した結果であると視覚的に解釈した。その結果、彼はx=0での発散とx=0での収束値とx>0からx=0への収束値を図示の中で視覚的に発見した。

おまけ

以下では、筆者はおまけを提示する。

一般化

【視覚的な予想4.1】
$n≧1$では、$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{n}exp(-kxcot(\frac{π}{2n+2}))cos(kx)$$は収束値（極限値）を持つ。その時、$$\sum_{k=1}^{∞}k^{n}exp(-k \cdot 0 \cdot cot(\frac{π}{2n+2}))cos(k \cdot 0)$$は無限である。

$n≦-2$では、$$\lim_{x \to +0}\sum_{k=1}^{∞}k^{n}exp(-kxcot(\frac{π}{2n+2}))cos(kx)$$は収束値（極限値）を持つ。その時、$$\sum_{k=1}^{∞}k^{n}exp(-k \cdot 0 \cdot cot(\frac{π}{2n+2}))cos(k \cdot 0)$$は無限でなく、その収束値（極限値）に一致する

$-2<n<1$では、$\lim_{x \to +0}\sum_{k=1}^{∞}k^{n}exp(-kxcot(\frac{π}{2n+2})))cos(kx)$の振る舞いは上記の予想に一致しない。

無限級数の項の順序の交換

【筆者の印象】
無限級数の項の順序を変えることは関数それ自体を取り替えることである。

筆者が無限級数の順序を変えるとき、無限級数の値も異なった。一般的には、足す順序を変えると、値が異なるのは奇妙に感じる。しかし、彼が順序の交換を$\lim_{x \to +0}\sum_{k=1}^{∞}kexp(-kx)cos(kx)$のような関数？の交換（取り替え）と考えるとき、この現象はそれほど不思議でない。彼は関数それ自体を取り替えるので、その取り替えに沿って、$x>0$から$x=0$への値も異なるように思える。発散も同様である。

例えば、$1+2+3+…$を$1+3+2+…$と交換することは杉山式$\sum_{k=1}^{∞}kexp(-kx)cos(kx)$を別の異なる式（関数和）にすることである。その結果として、$-\frac{1}{12}$が$x>0$から$x=0$へと近づかなくなる。そのため、無限級数は別の収束値を取るようになる。