楕円
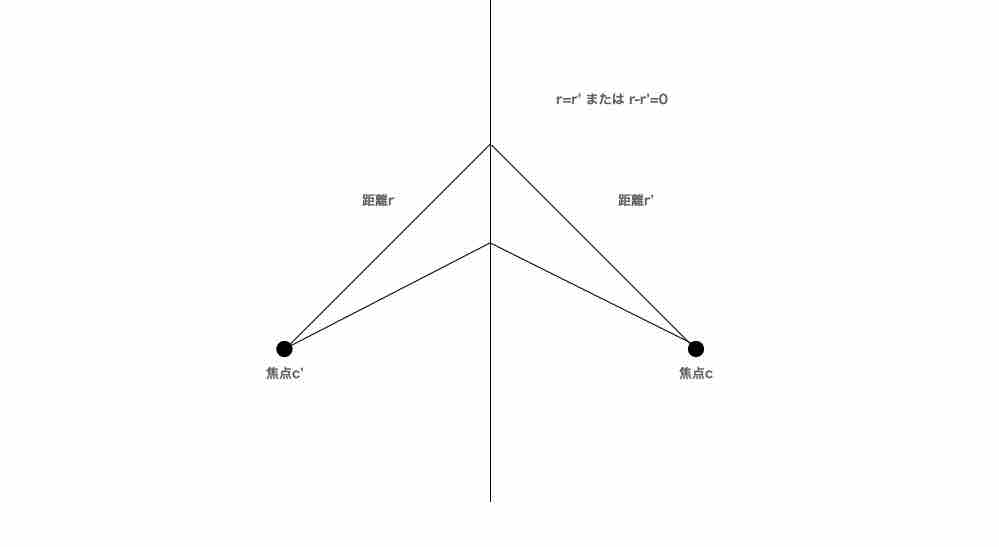
俺は二定点(焦点)を用意する。その後、俺は点Pを取る。俺はその点と二定点との距離r、r’を取る。俺は二つの距離が互いに等しくなるように設定する。r=r’、またはr-r’=0である。このとき、その点全体は直線になる。距離rは一定でない。当然、r/r’=一定も。
次に、俺は二つの距離の和が一定になるように、点Pを動かしたい。俺がその点を上へと運動させると、距離の和は長くなるように変わる。俺が点を真横へと運動させると、距離の和は長くなるように変化する。俺が点を下へと運動させると、距離の和は短くなるように変化する。しかし、俺がその点を楕円方向へと運動させると、二つの距離の和が一定になる。だから、楕円では、二つの距離の和が一定である。和が一定の場合、一方を伸ばすと、もう一方が縮むように点を運動させる。
さらに、俺は双曲線を考える。俺が点Pを左にずらすとき、rはr’よりも大きなる。そのとき、俺は二つの距離の差を考えることができるようになる。俺はこの差を一定にして運動させる。俺は点を焦点間に便宜的に置いて想像する。俺がこの点を左や右を含む横へと運動させると、差が変化する。左に運動させると、差は大きくなる。右に少し移動させると、差は小さくなる。また、俺が点を上へと少し移動させると、その差は少し大きくなる。だから、俺は点Pを左斜め方向へと移動させて、その差を一定に保つ。すると、双曲線が描かれるように思える。左斜めに移動させると、距離rも距離r’も同様に大きくなるので、差が一定に保たれると予想する。差が一定の場合、一方を伸ばすと、もう一方も伸びるように点を運動させる。