 西洋文明(欧州+地中海)
西洋文明(欧州+地中海) ポピュリズム(大衆主義)とは何であるのか?〜日本の例〜
ポピュリズム(大衆主義)は主義である、かつそれはある主体が大衆に迎合することである。ポピュリスト(大衆主義者)は人間である、かつそれは大衆に迎合する。 筆者はポピュリズムを大衆迎合主義とも訳する。彼はポピュリストを大衆主義者と訳する。以下で...
 西洋文明(欧州+地中海)
西洋文明(欧州+地中海)  言語
言語  言語
言語  言語
言語  コーカサス人種
コーカサス人種 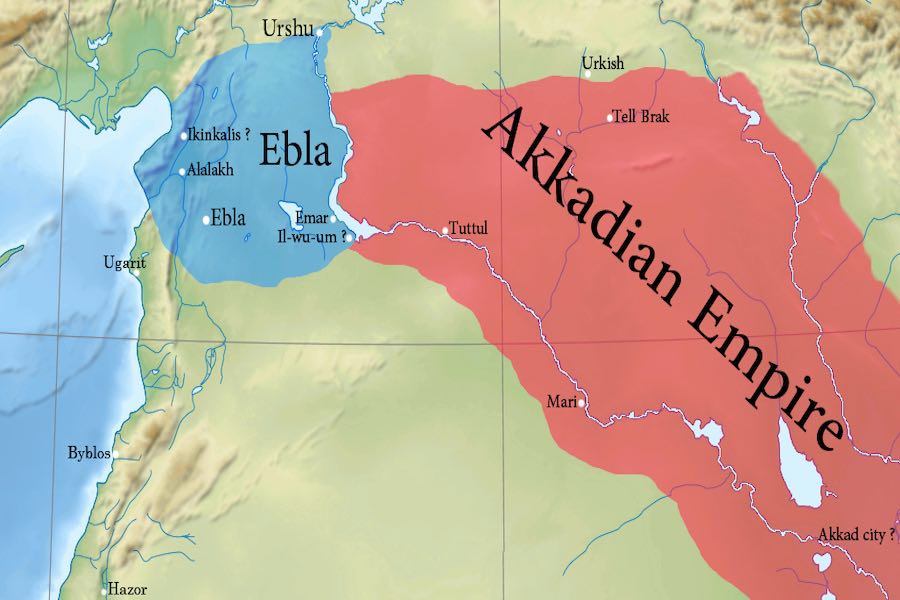 コーカサス人種
コーカサス人種  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  コーカサス人種
コーカサス人種  言語
言語  言語
言語 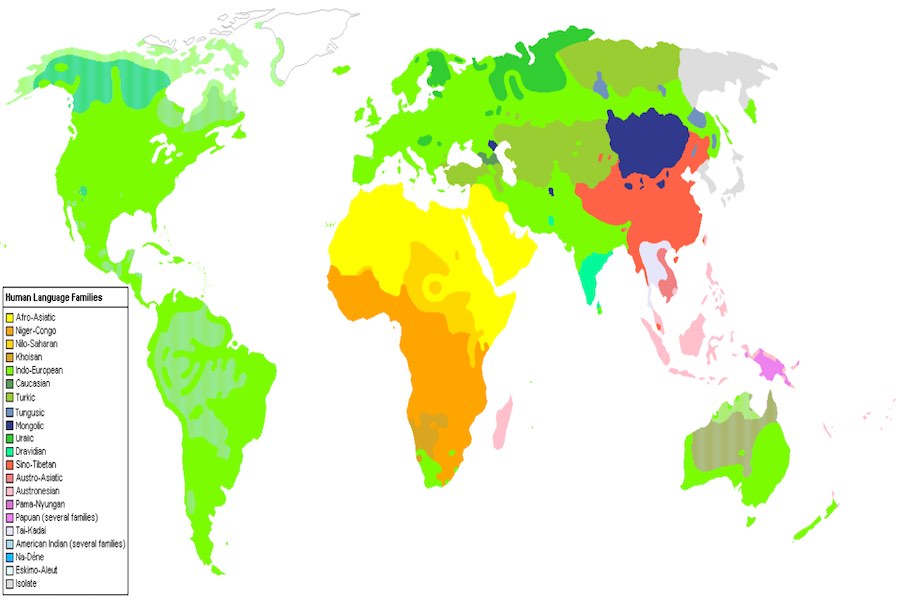 言語
言語 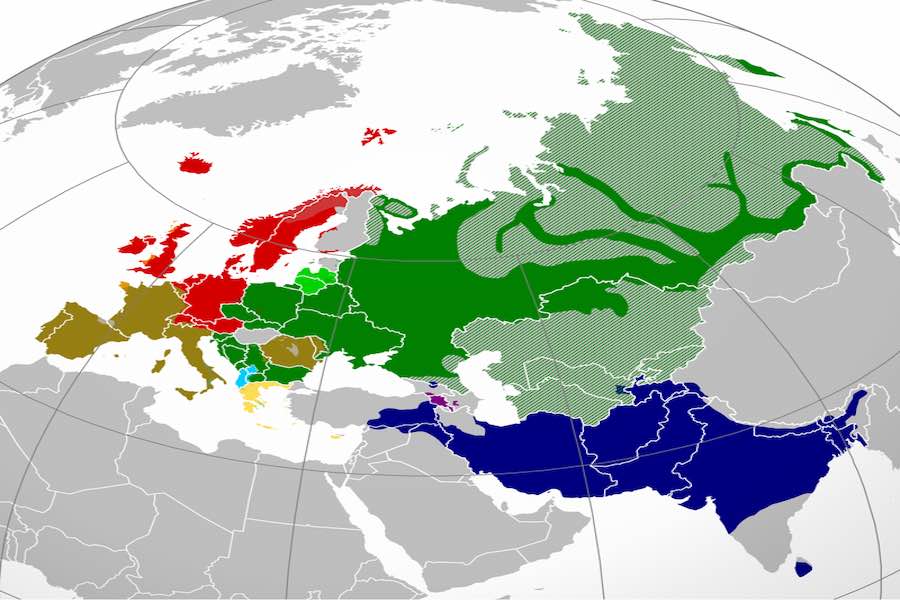 言語
言語  言語
言語  言語
言語  言語
言語 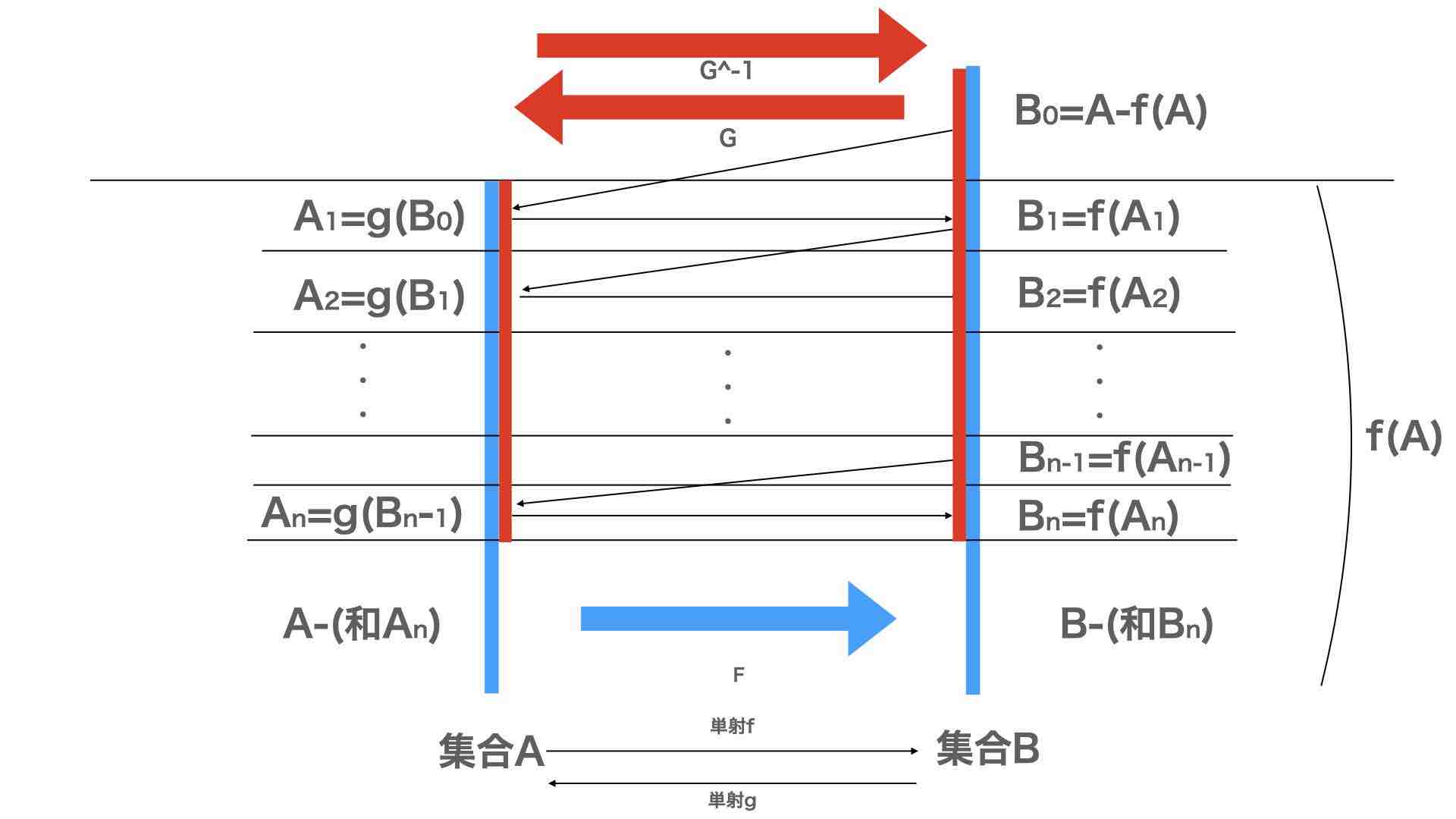 言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  歴史(目的別)
歴史(目的別)  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  カタカナ用語
カタカナ用語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語  言語
言語