ベルンシュタインの定理(ベルンシュタインのていり、カントール=ベルンシュタイン=シュレーダーの定理、シュレーダー=ベルンシュタインの定理、カントール=ベルンシュタインの定理とも、英: Schröder–Bernstein theorem)とは、集合 A から集合 B に単射 があり、集合 Bから集合 A へも単射があれば、集合 A から集合 B への全単射があるというものである。濃度においては、これは |A| ≤ |B| かつ |B| ≤ |A| ならば |A| = |B| である、ということを言っているわけで、非常に基本的な要請がこの定理によって満たされることになる
https://ja.wikipedia.org/wiki/ベルンシュタインの定理
以下では、俺はベルンシュタインの定理、またはシュレーダー=ベルンシュタインの定理に対する俺の現時点での認識を提示するつもりである。盛大に間違っている可能性が高いので、上記の図も含めて、十分に注意して。下記の情報は俺の認識であり、ベルンシュタインの定理それ自体でない。俺は[0, 1]と[-1, 1]と混同していた。
背景
・背景
俺は閉区間[-1, 1]と実数全体の集合Rとの対応関係を知りたい。開区間(-1, 1)と実数全体の集合Rの場合、俺はx/(1-x^2)を取ると、俺はその開区間からRへの全単射を発見することができる。この時、開区間(-1, 1)はRに対等である。しかし、俺は閉区間[-1, 1]と実数全体の集合Rとの対応関係を同じような方法で知ることができない。そこで、俺は集合Aと集合Bとの対応関係を一般的に知るための方法を考える。
・前提
個人的な印象では、俺は次の前提を提示する。その前提とは、2つの対象のそれぞれの長さや差は二つの対象間の対応と異なることである。
例えば、線分10と線分1が存在して、整数点を持つ。線分1は0ー1であり、線分10は0ー1ー…ー9ー10である。線分10と線分1は互いに異なる長さを持つ。けれども、俺は線分の中の有理数を考える時、もし俺が線分10の整数点を10分の1にするような対応(1/10)xを考えるならば、一対一の対応関係が線分10と線分1との間に存在する。0は0、1は1/10、2は2/10、…9は9/10、10は10/10=1である。つまり、線分10と線分1は互いに異なる長さを持つが、一対一の対応関係が線分10と線分1との間に存在する。
だから、俺はたとえ2つの対象の長さが異なるとしても、一対一の対応関係はその2つの対象につくかもしれないと憶測する。俺はこの考えを閉区間[-1, 1]と実数全体の集合R、または実数直線との対応へと拡張して、一対一の対応関係が存在するのかを調べる。実数直線は閉区間[0, 1]よりも非常に長いが、一対一の対応関係がつくことは想定内の範囲であるようにも感じる。
ベルンシュタインの定理
集合Aと集合Bが存在する。また、集合Aの部分集合A1と集合Bの部分集合B1が存在する。aは集合Aの要素である。bは集合Bの要素である。
・ベルンシュタインの定理
俺系統の認識 ベルンシュタインの定理とは、次である。もしある集合Aからある集合Bへの単射が存在して、かつ集合Bからある集合Aへの単射が存在するならば、集合Aは集合Bに対等である。
対等(equipotent)とは、集合Aと集合Bとの間に、少なくとも一つの全単射が存在する。俺は閉区間[0, 1]とRとの間に全射が存在するのかを知ることができない。感覚的には、Rの中の点の数はその閉区間の中の点の数よりも多いように感じてしまう。だから、俺は閉区間からRへの全射がない可能性があると感じてしまう。同時に、俺は開区間(-1, 1)とRとの全単射を考え得ることができた。だから、俺は閉区間[-1, 1]は開区間(-1, 1)よりも点の数が多そうであるので、俺は閉区間[-1, 1]とRとの全射、または全単射も考えることができるように感じる。
単射の終集合を縮小させる時、俺は単射を全単射に変化させることができる。なぜなら、俺はbの逆像が空であるようなbを排除することができる。そこで、俺は上記を次の形に変形する。
俺系統の認識 もし部分集合A1が集合Bと対等であり、かつ部分集合B1が集合Aと対等であるならば、集合Aと集合Bは対等である。
例えば、閉区間[-1, 1]と実数全体の集合Rが存在する。俺は開区間(-1, 1)を閉区間[-1, 1]の部分集合として取る。俺は閉区間[-1, 1]をRの部分集合として取る。この時、開区間(-1, 1)はRと対等であり、かつRの閉区間[-1, 1]は閉区間[-1, 1]それ自体と対等である。だから、閉区間[-1, 1]は実数全体の集合Rと対等である。
証明
俺は上記の証明を全く理解できない。俺は俺の現時点での認識を提示するつもりである。俺は集合Aと集合Bを考える。俺は集合Aから集合Bへの単射fと集合Bと集合Aへの単射gを考える。俺は単射をタと表示する。また、集合Aから集合Bへの単射では、集合Aの要素の全てが集合Bへと写像されるらしい。個人的な勘違いとして、俺は単射では、写像されない要素があっても良いと感じていた。しかし、単射では、集合Aにおける任意の要素は写像されるらしい。
・証明
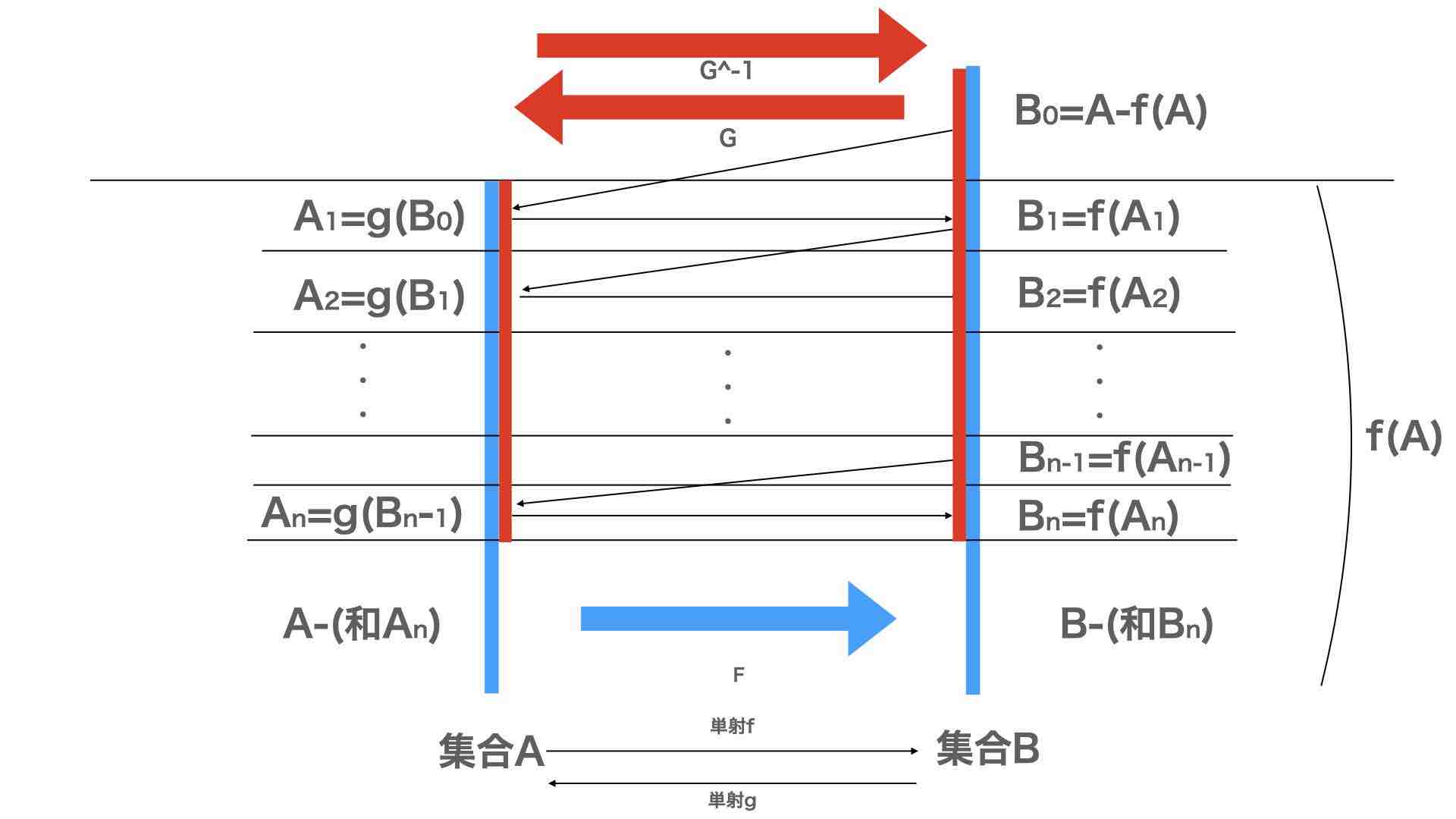
まず、俺は集合Aから集合Bへの単射fを考える。f(A)が生じる。Aからf(A)への写像それ自体はすでに全単射であるかもしれない。閉区間[-1, 1]とRとの単射を考えるとわかるように、単射されない要素bが存在する。一方で、閉区間[-1, 1]とf([-1, 1])自体は全単射であるかもしれない。俺はこのb全体の集合をB0(打たれていない領域)と置く。打たれていない領域は初めに単射されなかった領域である。例えば、閉区間[-1, 1]とRでは、b=100^100は写像されない要素であるかもしれない。
次に、俺は集合Bから集合Aへの単射gを考える。俺は集合AへのB0(打たれていない領域)の単射gを考える。すると、単射された要素aが存在する。俺は要素a全体をA1(単射領域)と置く。g(B0)=A1。この時、B0の要素の全ては単射されているはずである。俺がRにおけるB0を考えると、B0から閉区間[-1, 1]への単射が存在するのかは不明であるように感じるが、おそらく単射の存在それ自体が仮定されているように見える。感覚的に捉えると、B0から閉区間[-1, 1]への単射?は重複して単射にならないように感じる。
この操作を繰り返していくと、B0(打たれていない領域)から単射された領域が集合Aと集合Bの中に存在することになる。単射における終集合を縮小させると、これらの単射は全単射であるとみなせるかもしれない。俺はこの領域を(打たれていない領域から単射された)単射領域と便宜的に呼ぶ。俺は集合Aにおける単射領域の和集合と集合Bにおける単射領域の和集合を考える。
さらに、俺は集合Aにおける単射領域の和集合を集合Aから引く。俺は集合Bにおける単射領域の和集合を集合Bから引く。すると、B0からの単射に無関係な領域が集合Aと集合Bに残る。俺はこれらの領域を無関係領域(または安全領域)と便宜的に呼ぶ。この時、集合Aにおける無関係領域の単射fは集合Bにおける無関係領域に対応する。集合Bにおける単射領域の単射gは集合Aにおける単射領域に対応する。
俺はこの単射fの定義域を集合Aから集合Aにおける無関係領域に縮小させ、終集合を集合Bにおける無関係領域に縮小させる。この時、この単射fは全単射になる。俺はこのfをFと置く。同様に、俺はこのgの定義域を集合Bから集合Bにおける単射領域に縮小させ、終集合を集合Aにおける単射領域に縮小させる。この時、この単射gは全単射になる。俺はこのgをGと置く。の逆像G^-1を考える。この時、俺は次の写像を獲得する。
俺系統の認識 俺は次の写像を考える。もしaが無関係領域に所属するならば、F(a)。もしaが単射領域に所属するならば、G^-1(a)。
上記が全単射である。だから、集合Aと集合Bは対等である。個人的な印象では、俺は単射される領域とそうでない領域に分割する。その後、そうでない領域の単射を次々と考えていく。俺はその領域の和集合を取り、その和集合と残りの集合に分割する。単射されていった和集合同士の写像と残りの集合同士の写像を別々に考える。すると、別々の写像はそれぞれ全単射になる。俺がこの写像をまとめると、全単射を得る。
例えば、閉区間[-1, 1]とRが存在する。単射fと単射gを考える。俺はRへの閉区間[-1, 1]の単射を考える。すると、Rには、単射されない領域B0が生じる。単射された領域は部分的には全単射であるはず。さらに、俺は閉区間[-1, 1]へのこの領域の単射gを考える。すると、閉区間[-1, 1]には、gに単射された領域が生じる。単射された領域は部分的には全単射であるはず。これを繰り返していくと、閉区間[-1, 1]とRは、それぞれ、領域B0から単射された領域と領域B0から単射されない領域に分割される。俺は領域B0から単射された領域同士の対応と領域B0から単射されない領域同士の対応をそれぞれ考える。その対応のそれぞれは全単射になるので、集合Aは集合Bに対等である。
・閉区間[0, 1]とR
俺は閉区間[0, 1]とRを用意せよ。俺は閉区間[0, 1]からRへの単射fを用意せよ。俺はRから閉区間[0, 1]への単射gを用意せよ。今、俺は単射fを想像せよ。この時、Rには、単射されない要素達B0が存在する。もしRへの閉区間[0, 1]の単射がRの要素の全てに対応するならば、その単射は全単射である。
ここでは、俺は閉区間[0, 1]からRへの全単射を人工的に構成したい。そこで、俺は閉区間[0, 1]とRを二つの部分に分割する。その後、俺は二つの写像をそれぞれの部分に与えて、全単射を人工的に構成する。俺は「単射されない要素達に関係する写像」と「そうでない要素達に関係する写像」の二種類を考える。言い換えると、「f([0, 1])で余った部分に関係する写像」と「そうでない要素達に関係する写像」の二種類を考える。
今、俺はg(B0)を考える。g(B0)は閉区間[0, 1]の部分集合A1である。g(B0)の終集合を縮小すると、B0とA1は対等である。B0〜A1。同様に、f(A1)を考える。f(A1)はRの部分集合B1である。A1はB1は対等である。A1〜B1。A1はB0に対等であるので、B0はB1にも対等である。だから、B0〜A1〜B1。この操作を繰り返すと、俺はAnやBnを獲得する。すると、B0〜A1〜B1〜…〜An〜Bn。並べ変えてみると、A1〜A2〜…〜An。B0〜B1〜…〜Bn。これらの和集合を取ると、俺は∪Anと∪Bnと獲得する。それぞれの集合は(内部とも外部とも)対等であったので、∪Anと∪Bnも対等であるように感じる。もしそうであるならば、∪An〜∪Bn。
上記では、俺は閉区間[0, 1]からRへの全射を構成することができなかった。しかし、余りの部分(単射されない要素達B0)の単射を考えていくと、余りの部分に関するR側から閉区間[0, 1]側への全単射を考えることができるようになった。この時、もし余りの部分に関係ない閉区間[0, 1]及びRに関する全単射も考えることができるならば、その時、俺は閉区間[0, 1]からRへの全単射を人工的に構成することができる。ただし、その全単射はもしnが偶数であるならば、aであり、nが奇数であるならb、bであるように二つの部分、または二つの条件から構成される。
実際、俺は∪Anを閉区間[0, 1]から差し引け。[0, 1]ー∪An。俺は∪BnをRから差し引け。Rー∪Bn。俺は[0, 1]ー∪AnからRー∪Bnへの単射を考えよ。俺は終集合を縮小させよ。すると、俺は[0, 1]ー∪AnからRー∪Bnへの全単射を獲得するだろう。
・怪しいたとえ
西軍と東軍が存在する。西軍から東軍への単射的射撃fが存在する。西軍の兵士には、0から1までの実数の番号が振られている。東軍には、実数の番号が振られている。東軍から西軍への単射的射撃gが存在する。もし西軍と東軍の兵士が単射的射撃を実行するならば、彼らの全ては射撃を実行する。
今、西軍の兵士の全てが射撃fを実行する。すると、東軍には、撃たれた兵士と撃たれていない兵士B0(兵士の集合B0)が存在する。西軍の兵士の全てと撃たれた兵士との対応は一対一の対応(全単射的射撃)である。もし東軍の撃たれていない兵士が存在しなかったならば、その時、その射撃は全単射的射撃である。
次に、東軍の撃たれていない兵士の全てが単射的射撃gを西軍へと実行していたとする。すると、西軍には、撃たれた兵士達が存在している。この撃たれた兵士達は撃った兵士でもある。東軍の撃たれていない兵士B0と西軍の撃たれた兵士A1との対応は一対一の対応(全単射的射撃)である。
さらに、西軍の撃たれた兵士A1が単射的射撃gを東軍に実行していたとする。この時、兵士A1による単射的射撃fは撃たれていない兵士B0(兵士の集合B0)を撃たない。なぜなら、初めの射撃fにおいて、兵士B0は撃たれなかった兵士である。だから、f(A1)はB0の部分集合でなく、f(A)の部分集合である。一般的には、f(An)⊂f(A)。
これを繰り返すと、初めに撃たれていない兵士B0から撃たれてきた兵士とそうでない兵士が東軍と西軍のそれぞれに生じる。この時、俺は西軍におけるそうでない兵士と東軍におけるそうでない兵士との単射的射撃fを考える。さらに、俺は東軍におけるB0と兵士B0から撃たれてきた兵士と西軍における兵士B0から撃たれてきた兵士との単射的射撃gを考える。この時、俺は終集合を縮小させると、全単射的射撃fと全単射的射撃g、そしてその逆像g^-1と考えることができる。
電飛
ちゃんとした情報を知りたい場合、次をみよ。俺は上記の情報を正しいと主張しない。