集合(しゅうごう、英: set, 仏: ensemble, 独: Menge)とは数学における概念の1つで、大雑把に言えばいくつかの「もの」からなる「集まり」である。集合を構成する個々の「もの」のことを元 (げん、英: element; 要素) という。
https://ja.wikipedia.org/wiki/集合
以下では、著者は集合が何であるのかを提示する。一般的には、集合は”ものの集まり”と考えられる。そして、その集まりは幾何学的な曲線で表示されている。 なお、下記では、謎の考えが提示される。ちゃんとした教科書を読もう。
1.0 定義
以下では、筆者は集合の定義を提示する。彼は日常的な推論を提示する。
1.1 定義
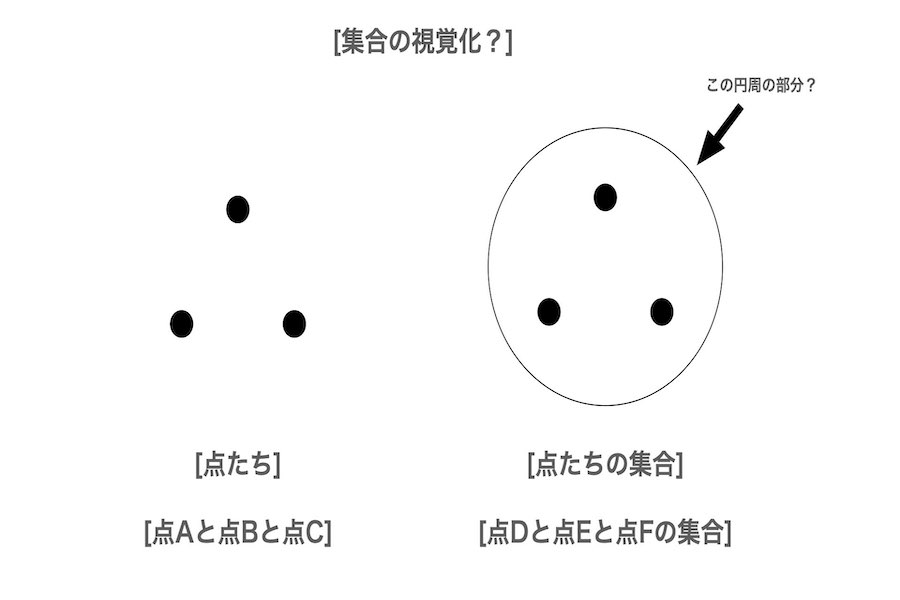
1.1(俺系統の認識) 集合は対象を所属させる空間である。
または、集合は対象を所属させる入れ物である。要素は空間(集合)に所属する対象である。または、集合は対象を所属させる入れ物と空間(入れ物)に所属する対象の組である。もしある対象がある集合に所属するならば、その対象はその集合のある要素である。つまり、ある対象がある集合の要素であるとは、その対象はその集合に所属することである。
日常的には、要素はある対象aを構成する対象bである。幾何学的には、集合は対象たちを囲む曲線や曲面である。なお、対象たちそれ自体は集合でない。筆者は対象たちを認識した後、彼は対象たちの集合を考える。
では、なぜ彼は集合を考える必要があるのだろうか?ここでは、彼は集合がない状態や所属がないを考えてみる。今、西欧白人と結婚した日本モンゴロイド人の雌を考えてみる。彼女は結婚した後、夫と中間種の子供を連れて、「欧米では、男女平等で二重国籍が認められている。それに対して日本ではそうでない。日本は遅れている」と発言した。
このように、日本モンゴロイド人の雌は西欧白人と結婚したのにも関わらず、彼らは大和民族の父系社会にわざわざ入ってくる。そして、彼女らは西欧キリスト教系統の教えを大和民族の儒教系統の父系社会の中で披露して、見せびらかそうとする。なぜなら、彼女は社会(society)や所属それ自体を認識していない。この時、彼は日本人男性たちの集合を形成して、その雌の侵入、または越境を防止する。
また、大和民族自身も彼ら自身が東洋文明に所属しているのか、西欧文明に所属しているのかを自己認識していない。なぜなら、彼らは”文明の集合”を認識していない。そのため、彼らは法や国家システムや統治制度に関して西欧と東洋の都合の良い部分のみをデタラメに引用して、彼らの意見もどきを形成しようとする。さらに、彼は西欧と東洋を都合よく行き来しようとする。この状態では、会話も文明の形成もできないので、彼は文明の集合、つまり境界をはっきりと定めようとする。
2.0 数の集合
以下では、彼は数の集合を考える。彼は個数を、1を-alk、2を-ilk、3を-ulk、…と置いていく。彼は順序を1を-als、2を-ils、3を-uls、…と置いていく。彼は0を-rekや-relsと置く。正負は-s-と-f-で表現される。例えば、ある点はpointalkalsのように表現される。日本語では、点1個1番。正の点はpointsalkalsのように表現される。
分数について、彼は考えていない。現時点では、彼は分数を-lakのようにaとlを逆転させて表現する。例えば、2/3はpoint-luk-ilkalsである。-は見やすさのために使用した。順序では、pointalk-lus-ils。分数では、彼は2.3をpoint(il and mok-ulk)alsのように表現する。
2.1 数の集合と点の集合
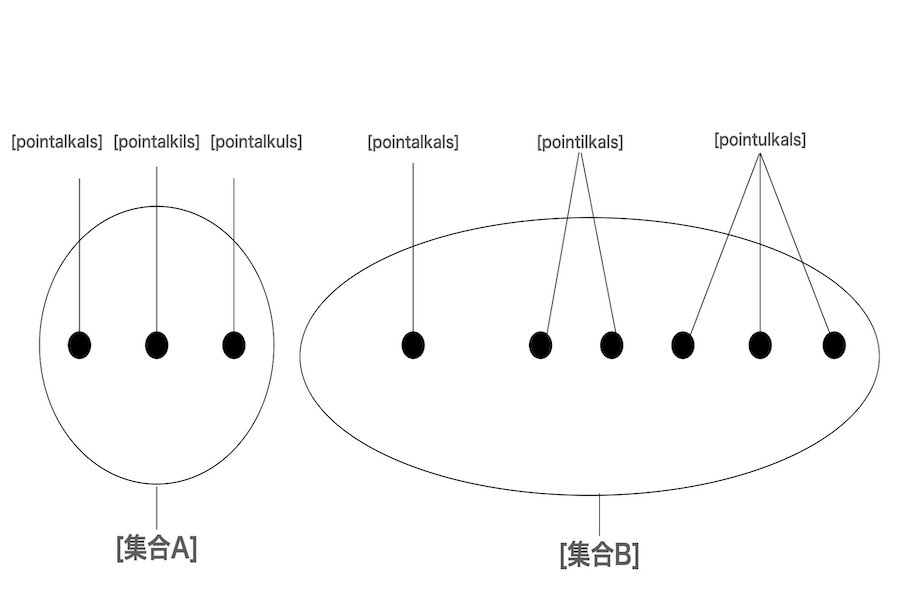
今、彼は1と2と3の集合を考える。一般的には、この集合は数字の1と2と3の集合で表現されている。ここで、彼は次の2通りを考える。一番目は、pointalkalsとpointalkilsとpointalkulsの集合Aである。二番目は、pointalkalsとpointilkalsとpointulkalsの集合Bである。前者は点の順序に関する集合である。後者は点の個数に関する集合である。後者は合計して、pointamkalsとも表現される。
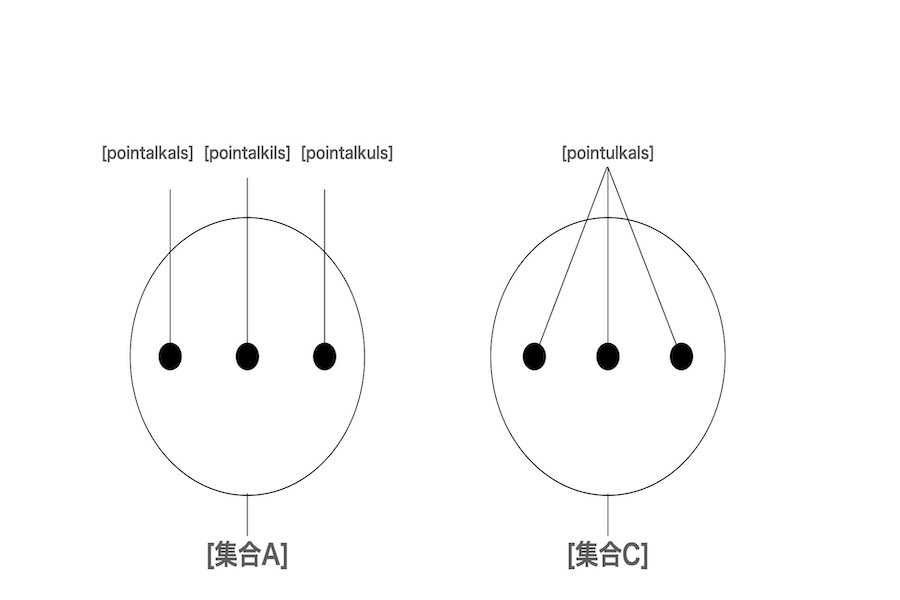
幾何学的には、pointalkalsとpointalkilsとpointalkulsの集合Aはpointulkalsの集合Cに等しい。演算としても、pointulkalsはpointalkals+pointalkils+pointalkulsに分解される。
一般化すると、pointxlkals=pointalkals+pointalkils+…+pointalkxls。xは未知数である。
2.2 空集合
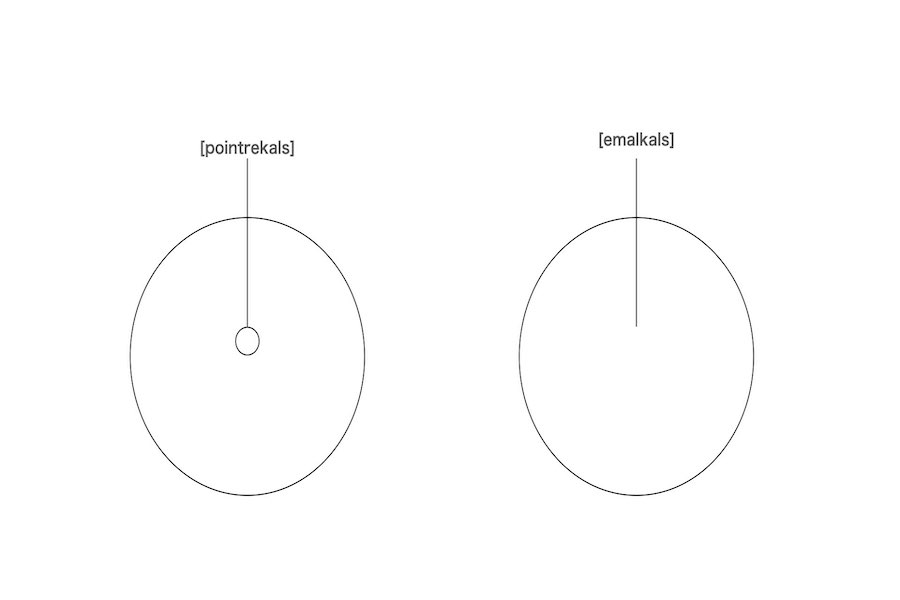
空集合は集合である、かつその要素は存在しない。例えば、彼はpointrekalsの集合を考える。幾何学的には、この集合の中には、何も入っていないが、これは空集合でない。pointrekalsが存在する。彼は空をkara-alklas(またはem-alkals)で表現する時、kara-alklasが存在する。
日常的には、幽霊会社が空集合のように思える。
2.3 無限集合
無限集合は集合である、かつその要素の数は無限である。有限集合は集合である、かつその要素の数は有限である。無限集合には、pointalkalsとpointalkilsとpointalkulsと…の集合Mがある。また、pointinfilkalsの集合Nがある。なお、彼は無限を-infiと表現する。Mの要素の和を考えると、そのMはNになる。Nの分解及び分離を考えると、そのNはMになる。
例えば、著者の認識では、無限個の点からなる図形はpointinfilkalsの集合Nである。
3.0 二つ以上の集合の状態
以下では、著者はいつ2つの集合が等しいのかを考える。また、彼はある集合が別の集合の部分であることを考える。彼は集合Aと集合Bを仮定する。個人的な印象では、集合を考えるとき、ある対象がある集合に所属するのかを考える。所属すれば、その対象は要素である。
また、彼はxを変数と仮定する。このxは金貨やips細胞のような何かである、またはxは単語[x]としては存在するが、確定されるまで対応先が不明である。彼はこの変数をobjectalkxlsやobjectxlkals、またはpointalkxlsやpointxlkalsのように書く。
金貨やips細胞のたとえでは、彼はそれを任意の要素に交換することができる。ただし、彼はそれを集合に加える、または外部に置く必要がある。
3.1 相等
3.1(俺系統の認識) もしxが集合Aに所属するならば、そのxは集合Bにも所属する、かつxが集合Bに所属するならば、そのxは集合Aにも所属する
この時、集合Aと集合Bは互いに等しい。口語的には、2つの集合の要素が全く同じであるとき、その2つの集合は互いに等しいと言える。ただ、日常的には、上記は異なる。例えば、ある会社AとBが存在して、ある社員のみがそれらの会社に所属する。会社の名前は互いに異なるので、集合それ自体も異なる。しかし、要素は同じである。
著者の認識では、結合や分解を考えない限り、pointalkalsとpointalkilsとpointalkulsの集合Aはpointulkalsの集合Cに等しくない。なぜなら、pointalkulsは集合Cに所属しない。また、pointulkalsは集合Aに所属しない。
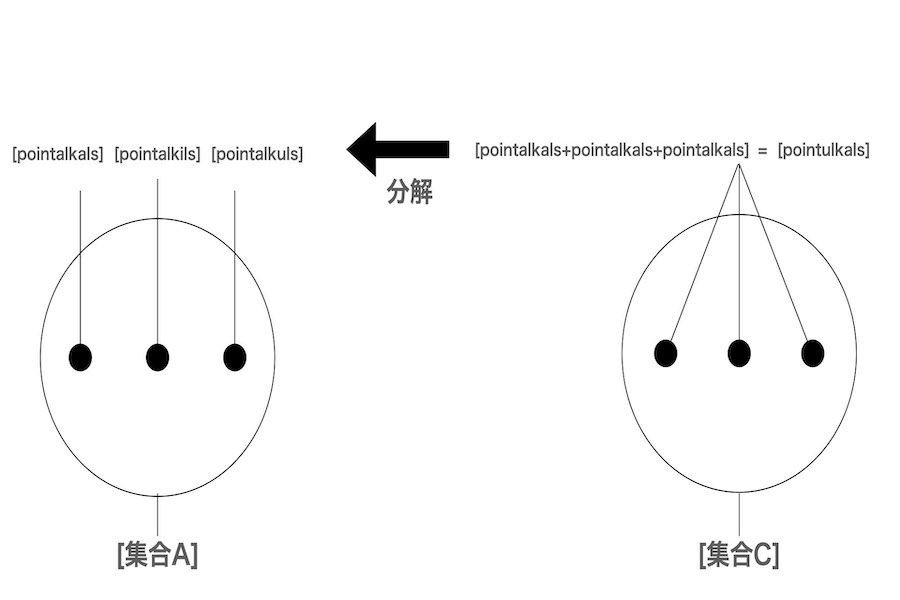
ただし、結合や分解を考慮すると、集合Aは集合Cに等しい。なぜなら、pointulkalsはpointalkalsとpointalkilsとpointalkulsの和(pointalkals+pointalkils+pointalkuls)である。これを分解すると、pointalkalsとpointalkilsとpointalkulsが得られる。これらは集合Aに所属する。また、集合Aの要素の結合を考えると、pointulkalsが得られる。それは集合Cに所属する。従って、集合Aと集合Cは互いに等しい、つまり相等である。
3.2 部分集合
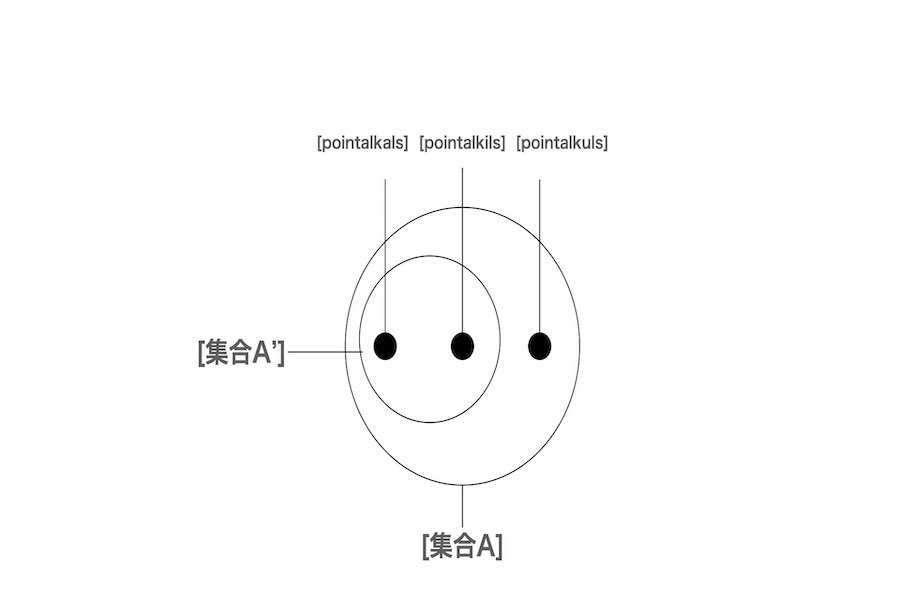
3.2(俺系統の認識) xが集合Aに所属するならば、そのxは集合Bに所属する。
この時、集合Aは集合Bの部分集合(部分)である。例えば、彼はpointalkalsとpointalkilsの集合A’を仮定する。この時、この集合は集合Aの部分集合である。しかし、結合や分解を考えない限り、この集合はpointulkalsの集合Cでない。
また、日常的には、心臓は人体の部分である。しかし、プラスティック製の心臓は人体の部分でない。なぜなら、心臓とプラスチック製の心臓では、それらの要素が互いに異なる。日常的には、ある臓器がある人体の部分であるのかは、その臓器がその人体で機能しているのかである。機能しているならば、それは部分である。
3.21(俺系統の認識) もし集合Aが集合Bに等しいならば、集合Aは集合Bの部分である、かつ集合Bは集合Aの部分である。
もしある主体がある集合Aが別の集合Bに等しいことを証明したいならば、その主体が集合Aは集合Bの部分である、かつ集合Bは集合Aの部分であるを証明する。


