以下では、俺はカントールの対角線論法に対する俺の現時点での認識を提示する。もし君がちゃんとした情報を知りたいならば、君は参考書を購入するか、職業数学者に尋ねよう。
カントールの対角線論法
カントールの対角線論法
俺は自然数の集合と実数の集合[0,1]を考える。なお、俺は(0.1]と[0.1]の違いを把握することができなかったので、俺は[0,1]を使用する。実数は十進数で表示されるので、俺は次の表示を獲得する。
f(1)=0.0000…………………………………………………………………………………………………………………
f(2)=0.0010…………………………………………………………………………………………………………………
f(3)=0.1000…………………………………………………………………………………………………………………
(省略)
f(n)=0.5000…………………………………………………………………………………………………………………
(省略)
f(m)=0.9999……………………………………………………………………………………………………………….
次に、俺は次の数列$b_n$を考える。その数列の少数第一の項は「もしf(1)の少数第1位が偶数であるならば、1である。もしf(1)の少数第一が奇数であるならば、0である。」である。上記の例では、$b_n$の少数第一は1である。
その数列の少数第一の項は「もしf(2)の少数第2位が偶数であるならば、1である。もしf(2)の少数第2位が奇数であるならば、0である。」である。上記の例では、$b_n$の少数第2位は1である。これを一般化すると、少数第nの項は「もしf(n)の少数第n位が偶数であるならば、1である。もしf(n)の少数第n位が奇数であるならば、0である。」である。
この時、$b_n$は上記のf(n)のどれでもない。なぜなら、$b_n$の少数第n位はf(n)の少数第n位と常に異なるので、$b_n$はf(n)でない。つまり、$b_n$の少数第1位はf(1)の少数第1位と異なるので、$b_n$はf(1)でない。$b_n$の少数第3位はf(3)の少数第3位と異なるので、$b_n$はf(3)でない。$b_n$の少数第3位はf(3)の少数第3位と異なるので、$b_n$はf(3)でない。これを繰り返すと、$b_n$はf(n)のどれでもない。
別な例?
俺は別な例を考える。上記では、俺は10進数を使用した。以下では、俺は2進数を使用する。
f(1)=0.0000…………………………………………………………………………………………………………………
f(2)=0.0010…………………………………………………………………………………………………………………
f(3)=0.1000…………………………………………………………………………………………………………………
(省略)
f(n)=0.1100…………………………………………………………………………………………………………………
(省略)
f(m)=0.111……………………………………………………………………………………………………………….
俺は次の数列$c_n$を考える。その数列の少数第1の項は「もしf(1)の少数第1位が0であるならば、1である。もしf(1)の少数第1位が1であるならば、0である。」である。上記の例では、$c_n$の少数第一位は1である。
上位と同様の操作を繰り返す。すると、数列$c_n$の少数第n位はf(n)の少数第n位と異なるので、その数列はf(n)と異なる。
無限の視覚化?
下記の話は非常に怪しい。俺は極限や収束や不等式に関する話を知らないと述べておく。俺は実数の十進法表示を視覚化した。おそらく、[0, 1]、または[0, 1)の実数が表現される。
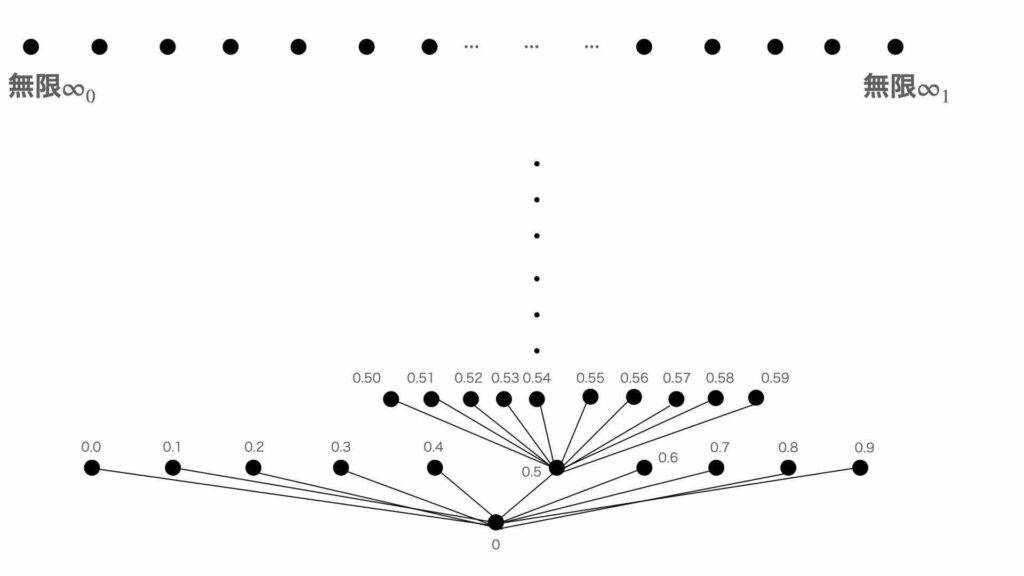
0.000…が無限$∞_0$である。0.999…が無限$∞_1$である。0.111…や0.333…は無限において黒丸として置かれる。前者は$∞_1$であり、後者は$∞_3$である。有理数の場合も、0.123123…のように繰り返されるので、無限において黒丸として置かれる。この黒丸は$∞_123$である。
一方、無理数は有理数ように繰り返されない。そのため、無理数は$∞_123$のように表示されない。無理数は$∞_123…$のようになる。このため、無理数は無限において黒丸として置かれない。感覚的には、有理数は道が一つに定まっているので、無限を黒丸として表示することができる。一方、無理数は道が定まっていないので、無限を黒丸として表示できない、または表示できるのかよくわからない。
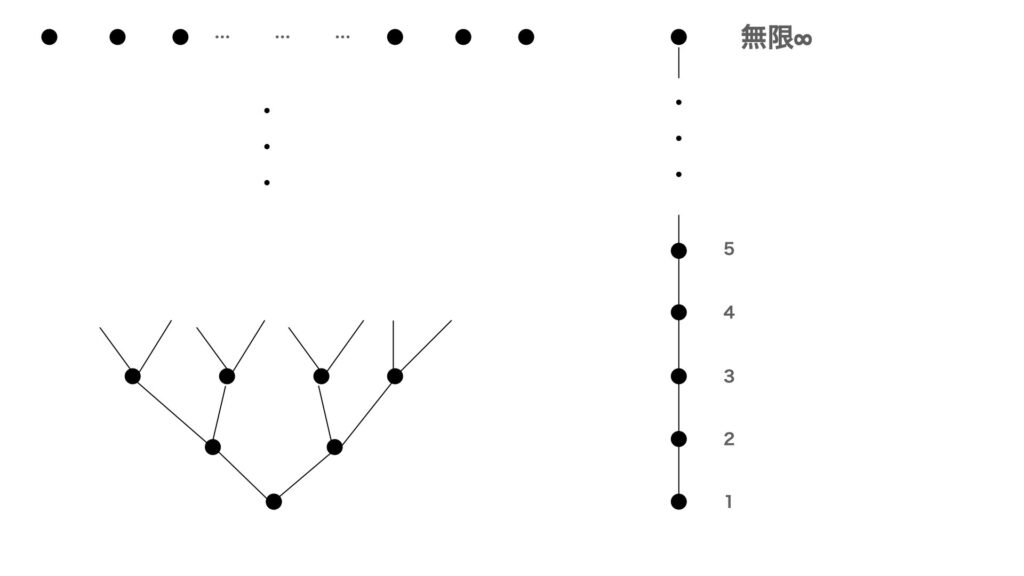
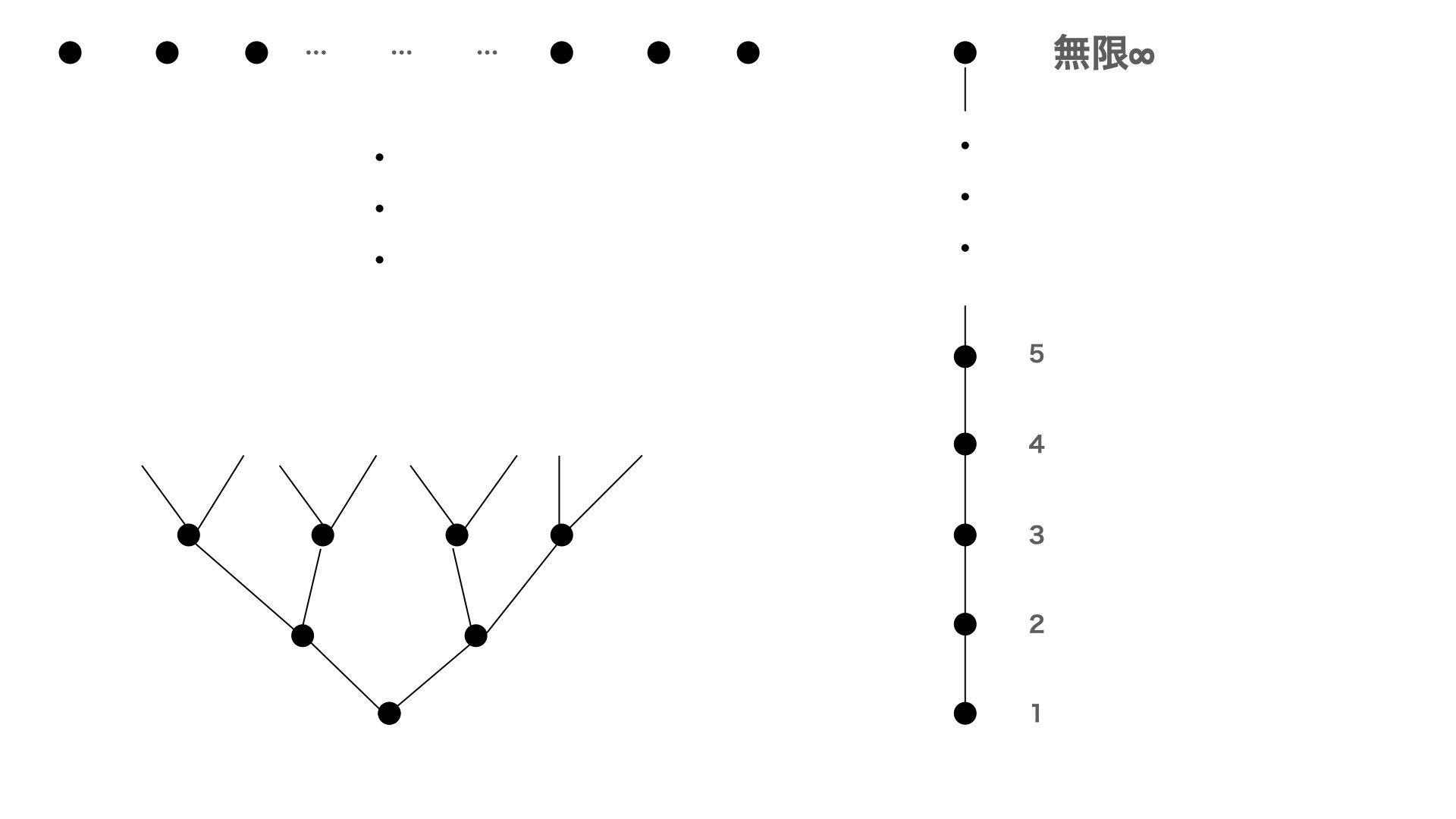
左は二進数?的である。右は自然数である。自然数では、無限が黒丸として定まっている。なぜなら、進む方向が常に一つであるので、無限が固定されていると解釈される?。一方、右はそうでない。一本道の場合、無限が定まる。または、もし進む道が固定されたならば、とある無限が定まる。
自然数の集合Nが右の形である。ある集合が図1の樹形図ように成っている場合、右の形との対応が存在しない可能性がある。左には、無限が何個もある。一方、右には、無限の数は1である。ただし、有理数の場合、無限における$∞_0$から$∞_1$への直線を考えて、図2の右の形との対応を考えることができるかもしれない。