数学において二つの集合 A, B の濃度が等しいとは、それらの間の一対一対応(全単射)が存在すること、すなわち A から B への写像f: A → B が存在して B の各元 y に対してちょうど一つづつの x ∈ A が f(x) = yを満たすときに言う[1]。濃度が等しいことは、それら集合に属する元の数が同じであることと解釈することができる[2]。
https://ja.wikipedia.org/wiki/等濃
盛大に間違っている可能性が高いので、十分に注意して。下記の情報は俺の認識であり、集合の対等に対する俺の認識それ自体でない。集合の対等における対等はequipotentである。
集合の対等
・定義(認識)
俺系統の認識 集合Aが集合Bに対等であるとは、集合Aから集合Bへの全単射が存在することである。
または、集合Aから集合Bへの全単射が存在するとき、集合Aは集合Bに対等である。あるいは、もし集合Aから集合Bへの全単射が存在するならば、集合Aが集合Bに対等である。名詞風の定義では、集合Bへの集合Aの対等(対等性)とは、集合Bへの集合Aの関係であり、そこでは集合Aから集合Bへの全単射が存在する。俺は関係を対応に置き換えることができるかもしれない。
対象
以下では、俺は分析される対象を提示するつもりである。個人的には、俺は数学とは、数学的な対象を分析する営みであると認識する。そこで、俺は分析される対象を何を分析するのかを明らかにするために提示する。なお、俺は閉区間の長さと閉区間の距離のどちらが正しいのかを知らない。
・自然数全体の集合と偶数全体の集合
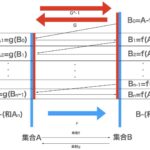
俺は自然数全体の集合Nを用意せよ。俺は正の偶数全体の集合Eを用意せよ。俺は正の偶数全体の集合Eと自然数全体の集合Nの間に一対一の対応(全単射)が存在するのかを分析せよ。俺が自然数全体の集合Nの要素を2倍するとき、俺は全単射2nを獲得する。
定義によると、集合Aが集合Bに対等であるとは、集合Aから集合Bへの全単射が存在することである。自然数全体の集合Nが正の偶数全体の集合Eに対等であるとは、自然数全体の集合Nから正の偶数全体の集合Eへの2nが存在することである。俺は2nを全単射と認識したので、俺は全単射という単語を2nで置き換えた(交換した)。とは〜の左と右が同じであると仮定すると、右の文が成立したので、左の文も成立する。
または、定義によると、集合Aから集合Bへの全単射が存在するとき、集合Aは集合Bに対等である。だから、自然数全体の集合Nから正の偶数全体の集合Eへの2nが存在するとき、自然数全体の集合Nは正の偶数全体の集合Eに対等である。左の条件節が成立したので、右の文も成立する。
・閉区間[0, 10]と閉区間[0, 1]
俺は閉区間[0, 10]と閉区間[0, 1]を用意せよ。閉区間[0, 10]の長さは閉区間[0, 1]の長さに一致しない。俺は閉区間[0, 10]と閉区間[0, 1]の間に一対一の対応(全単射)が存在するのかを分析せよ。俺が閉区間[0, 10]の要素を10分の1するとき、俺は全単射(1/10)xを獲得する。
定義によると、集合Aが集合Bに対等であるとは、集合Aから集合Bへの全単射が存在することである。閉区間[0, 10]が閉区間[0, 1]に対等であるとは、閉区間[0, 10]から閉区間[0, 1]への(1/10)xが存在することである。俺は(1/10)xを全単射と認識したので、俺は全単射という単語を(1/10)xで置き換えた(交換した)。とは〜の左と右が同じであると仮定すると、右の文が成立したので、左の文も成立する。
または、定義によると、集合Aから集合Bへの全単射が存在するとき、集合Aは集合Bに対等である。だから、閉区間[0, 10]から閉区間[0, 1]への(1/10)xが存在するとき、閉区間[0, 10]は閉区間[0, 1]に対等である。左の条件節が成立したので、右の文も成立する。
また、俺は上記を閉区間[a, b]と閉区間[c, d]に一般化せよ。さらに、俺は上記を開区間へと定義域及び終集合を縮小させて、一般化せよ。
・開区間(-1, 1)と実数全体の集合
俺は開区間(-1, 1)と実数全体の集合Rを用意せよ。開区間(-1, 1)の長さは実数全体の集合Rの長さに一致しない。俺は開区間(-1, 1)と実数全体の集合Rの間に一対一の対応(全単射)が存在するのかを分析せよ。俺が開区間(-1, 1)の要素をx/(1-x^2)するとき、俺は全単射x/(1-x^2)を獲得する。俺はこれが全単射であるのかを証明することができない。ただし、グラフを見ると、f(a)≠f(a’)で、f(a)=bとなるaが存在するように視覚的には見えるように感じる。
現象(定理)
・A〜A
俺系統の認識 集合Aは集合Aに対等である。
集合Aは集合Aに対等である。集合Aは集合Aに対等であるとは、集合Aから集合Aへの全単射が存在することである。俺はある全単射を恒等写像IAとせよ。その時、集合Aは集合Aに対等であるとは、集合Aから集合Aへの恒等写像IAが存在することである。右が成立するので、左も成立する。
・A~B→B〜A
俺系統の認識 もし集合Aが集合Bに対等であるならば、集合Bは集合Aに対等である。
もし集合Aが集合Bに対等であるならば、集合Aから集合Bへの全単射fが存在する。もし集合Aから集合Bへの全単射fが存在するならば、とある定理によって、集合Bから集合Aへの全単射f^-1が存在する。俺はその全単射f^-1を集合Bは集合Aに与えよ。その時、集合Bから集合Aへの全単射f^-1が存在する。集合Bは集合Aに対等であるとは、集合Bから集合Aへのf^-1が存在することである。右が成立するので、左も成立する。
使い方:使い方は次である。例えば、俺はある開区間とRとの対応関係を考える。俺は開区間(-1, 1)と考えるとき、俺はx/(1-x^2)という全単射を考えることができる。しかし、俺の脳では、俺はRから開区間(-1, 1)への全単射をパッと思いつかない。しかし、上記の定義を利用すると、俺はある開区間からRへの全単射を一つ考えれば十分であるように見える。
・A~B、B〜C→A~C
俺系統の認識 もし集合Aが集合Bに対等である、かつ集合Bが集合Cに対等であるならば、集合Aは集合Cに対等である。
もし集合Aが集合Bに対等であるならば、集合Aから集合Bへの全単射fが存在する。同様に、もし集合Bが集合Cに対等であるならば、集合Bから集合Cへの全単射gが存在する。とある定理によって、fとgの合成写像は全単射hである。集合Aは集合Cに対等であるとは、集合Aから集合Cへのhが存在することである。