多様体(たようたい、英: manifold, 独: Mannigfaltigkeit)とは、局所的にはユークリッド空間と見なせるような図形や空間(位相空間)のことである。
https://ja.wikipedia.org/wiki/多様体
以下では、創造主(著者)は多様体とは何であるのかを提示する。彼は上記の文章を理解することができなかった。直感的には、多様体は図形である、かつその図形は局所的にユークリッド空間である。ただ、たとえこの定義が彼に提示されるとしても、彼はこの定義の意味を把握しない。
1.0 多様体(manifold)〜背景と球面〜
1.1 背景
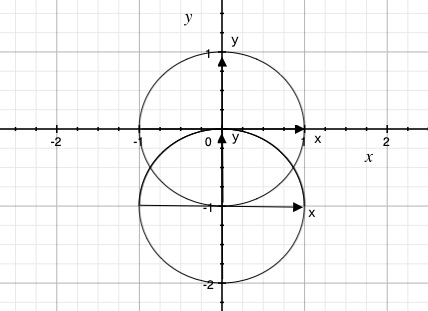
今、彼は上記のような2枚の円盤aとbを考える。上がaであり、下がbである。また、彼はx軸とy軸をそれぞれの円盤に便宜的に書くと仮定する。この時、彼は俺らは円盤aの縁を円盤bのx軸に重ね合わせることができない。
上記の画像がその様子である。下の円盤bの縁(円周)の部分は円盤aのx軸に重なり合っていない。この状態は当然であるように感じる。けれども、俺らが球面の上の円盤a及び円盤bを考える時、俺らは上記の円盤a及び円盤bの状態が必ずしも維持されるとは限らない。

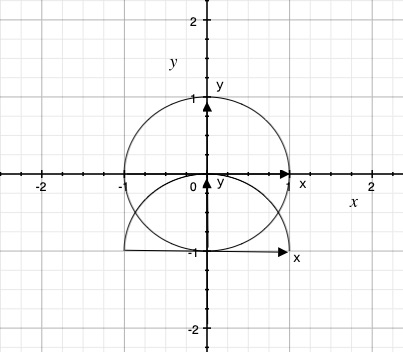
彼は緑の円盤をaとする。彼は手前の北極と南極の面をbとする。この時、球面では、円盤bの縁(円周)が円盤aのx軸に重なりあう。
上記の平面の場合、俺らは円盤bの縁を円盤aのx軸に重ね合わせることができなかった。しかし、球面では、彼は彼は円盤bの縁を円盤aのx軸に重ね合わせることができた。平面と球面では、円盤aと円盤bの重なり方が互いに異なることがわかった。
この時、彼はある空間の上の円盤たちの重なり方を調べることができるならば、その時、彼はその空間の性質も知ることができるかもしれないと期待する。なぜなら、空間の性質(情報)は円盤たちの重なり方に現れている。
彼は空間の上に貼られた円盤たち(座標たち)の貼り合わせ方を調べることができるならば、その時、彼は空間の性質を円盤たち(座標たち)の貼り合わせ方から知ることができる。上記では、多様体の定義には、局所的にはユークリッド空間であることが必要であった。なぜなら、局所的にはユークリッド空間であるとき、俺らは円盤たち(座標たち)に貼ることができる。
空間に貼られた円盤たち(座標たち)の貼り合わせ方が空間の性質を表している。だから、俺らがその貼り合わせ方を調べることができるならば、その時、彼は空間の性質も間接的に調べることができる。個人的な印象では、これが多様体的な考え方であるように感じた。
1.2 謎の計算
彼は具体的な計算を知らない。おそらく、3次元空間における円bの上半分が円aの下半分に重なり合うことを変換式で表示するかもしれない.。
1.3 擬球面と双曲

次に、彼は擬球面(電飛)を考えてみる。彼はこれが多様体であるのかを知らない。球面では、円盤bの縁は円盤aのx軸に重なったが、擬球面では、どのように重なるのだろうか?当然、彼はそれを予想できない。
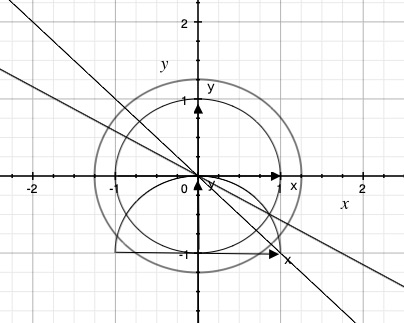
円盤bの縁がy=xや放物線になりそう。特に、馬の鞍では、円盤bの縁がy=xや放物線になりそう。
電飛
 | 価格:3,520円 |

