数学、特に解析学において変数(へんすう、英: variable[1])は、未知あるいは不定の数・対象を表す文字記号のことである。代数学の文脈では不定元(ふていげん、英: indeterminate)の意味で変数と言うことがしばしばある。方程式において、特別な値をとることがあらかじめ期待されている場合、未知数(フランス語版)(みちすう、英: unknown)とも呼ばれる。
https://ja.wikipedia.org/wiki/変数_(数学)
数学には、変数と未知数と不定元が存在する。筆者はこれらの違いを認識していない。以下では、彼はこれらが何であるのかを感覚的に提示する。
1.0 変数と未知数と不定元
始めに、彼は順序に関する未知の順序を考える。例えば、Japanese-alk-xls(日本人1個x番目)が存在する。Japanese-alk-xlsがJapanese-alk-ilsに等しいとき、Japanese-alk-xlsはJapanese-alk-ilsである。つまり、彼はxをiに交換する。
1.1(俺系統の認識) Japanese-alk-xlsは日本人である、かつJapanese-alk-xlsはJapanese-alk-ilsに等しい。
この時、上記の文が定めるxはiである。ここでのxはある順序と交換される。もし彼が文を形成しないならば、Japanese-alk-xlsにおけるxは任意である。この時、xは変数的である。彼はどの順番の日本人も取り出すことができる、または順序を任意に与えて表現することができる。ただし、順序が決定されている場合、彼はその順序を見た通りに表現する。
次に、彼は個数に関する未知の個数を考える。例えば、Japanese-xlk-als(日本人x個1番目)が存在する。Japanese-xlk-alsがJapanese-ulk-alsに等しいとき、Japanese-xlk-alsはJapanese-ulk-alsである。つまり、彼はxをuに交換する。
1.2(俺系統の認識) Japanese-xlk-alsは日本人である、かつJapanese-xlk-alsはJapanese-ulk-alsに等しい。
この時、上記の文が定めるxはuである。ここでのxはある個数と交換される。もし彼が文を形成しないならば、Japanese-xlk-alsにおけるxは任意である。この時、xは変数的である。彼はどんな人数の日本人も取り出すことができる。ただし、表現する場合は、彼が見たものを表現する必要がある。なぜなら、もし彼がJapanese-xlk-alsを実際に見るならば、彼が見ることはJapanese-xlk-alsにおけるxを定めることである。
さらに、彼は未知の種類について考える。x-alk-als(x種1個1番目)が存在する。彼は次の文を提示する。なお、-alsは-xlsでも良いかもしれない。
1.3(俺系統の認識) x-alk-alsはサピエンスである、かつx-alk-alsはY染色体ハプログループD1a2aを持つ。
上記の文は対象の種類を定める。例えば、彼がxを縄文人と置くと、上記の文は「jomonjin-alk-alsはサピエンスである、かつjoumonjin-alk-alsはY染色体ハプログループD1a2aを持つ」になる。上記の文が定めるxはjomojinである。ここでのxはある種類と交換される。この時、xは変数的である。もし彼が文を形成しないならば、x-alk-alsにおけるxは任意である。この時、xは変数的である。
まとめると、Japanese-alk-xlsやJapanese-xlk-alsやx-alk-alsは変数的である。xは何にでも変化する可能性がある。xは何にでも交換される可能性がある。しかし、彼が文を組む時、これらの単語におけるxは特定の対象に定まる。または、彼がある現象を見た通りに表現する時、これらの単語におけるxは特定の対象に定まる。この時、xは明らかでないが、xは文や見るという行為によって定まっている。このxが不定元的である。このxは定まっているが、解いて、xを具体的に明らかにする必要がある。
2.0 視覚化
ここでは、彼はxが何であるのかを感覚的に解釈して、その解釈を視覚化してみる。彼はxをips細胞やゴールドで例える。そして、彼はxという対象それ自体を人工的に組み込む。この時、文字としてのx([x])は紙幣に対応する。なお、ここでは、彼は単語をある対象に対応する対象(名札のような対象)と仮定した。
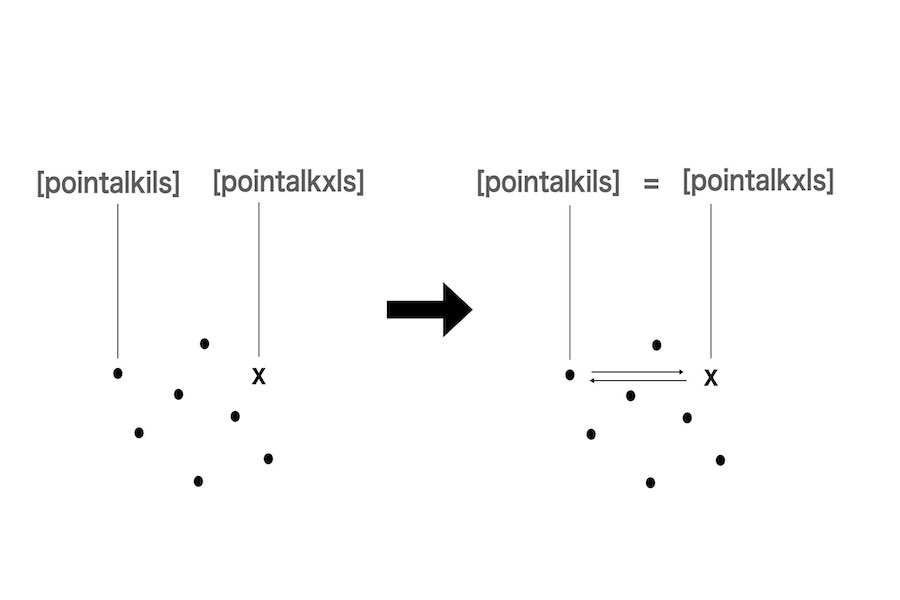
図2.1では、彼はxという対象(物体)を実際の点に中に人工的に組み込む。それに対して、彼は[pointalkxls]という名札を与える。その後、彼はxを最も左の点・[pointalkils]に等しくさせる。この時、xは・と交換される、または等しい、あるいは・に分化する。
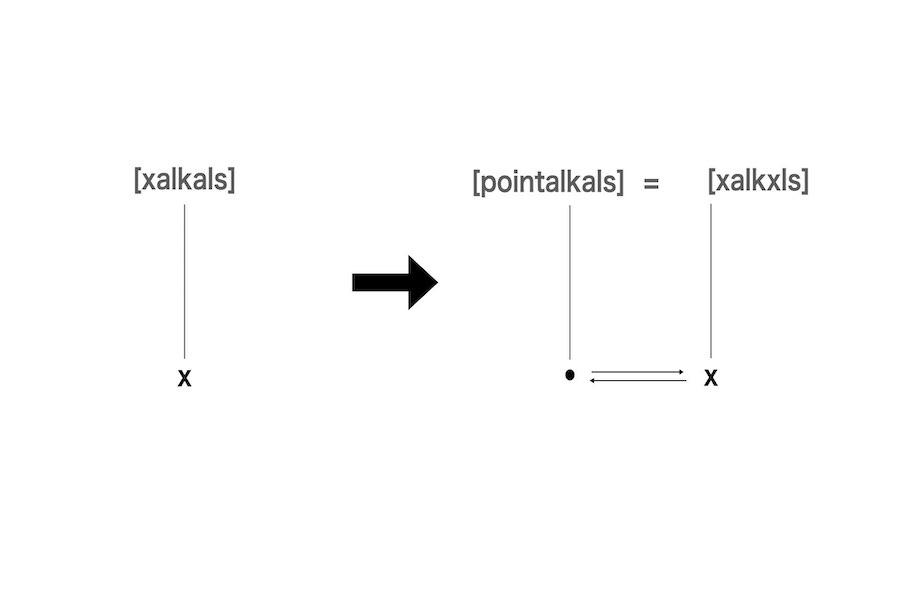
図2.1では、彼はxという対象(物体)を人工的に提示する。それに対して、彼は[xalkals]という名札を与える。その後、彼はxを最も左の点[pointalkals]に等しくさせる。この時、xは・と交換される、または等しい、あるいは・に分化する。上記の場合、「xalklasは点である、かつそれは〜である」という文で指定することもできる。


